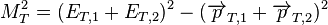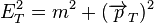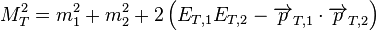Transverse mass

From Wikipedia, the free encyclopedia

The transverse mass is a useful quantity to define for use in particle physics as it is invariant under Lorentz boost along the z direction. In natural units it is:

$m_{{T}}^{2}=m^{2}+p_{{x}}^{2}+p_{{y}}^{2}\,$

where the z-direction is along the beam pipe and so

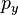$p_{x}$ and $p_{y}$ are the momentum perpendicular to the beam pipe and

$m$ is the mass.

Hadron collider physicists use another definition of transverse mass, in the case of a decay into two particles:

$M_{{T}}^{2}=(E_{{T,1}}+E_{{T,2}})^{2}-(\overrightarrow {p}_{{T,1}}+\overrightarrow {p}_{{T,2}})^{2}$

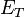where $E_{{T}}$ is the transverse energy of each daughter, a positive quantity defined using its true invariant mass $m$ as:

$E_{{T}}^{2}=m^{2}+(\overrightarrow {p}_{{T}})^{2}$

So equivalently,

$M_{{T}}^{2}=m_{1}^{2}+m_{2}^{2}+2\left(E_{{T,1}}E_{{T,2}}-\overrightarrow {p}_{{T,1}}\cdot \overrightarrow {p}_{{T,2}}\right)$

For massless daughters, where 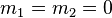$m_{1}=m_{2}=0$ , the transverse energy simplifies to $E_{{T}}=|\overrightarrow {p}_{T}|$ , and the transverse mass becomes

$M_{{T}}^{2}\rightarrow 2E_{{T,1}}E_{{T,2}}\left(1-\cos \phi \right)$

where $\phi$ is the angle between the daughters in the transverse plane:

A distribution of 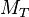$M_{T}$ has an end-point at the true mother mass: 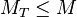$M_{T}\leq M$ . This has been used to determine the 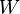$W$ mass at the Tevatron.

References

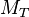J.D. Jackson (2008). "Kinematics". Particle Data Group. - See sections 38.5.2 ( $m_{{T}}$ ) and 38.6.1 ( $M_{{T}}$ ) for definitions of transverse mass.
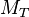J. Beringer et al. (2012). "Review of Particle Physics". Particle Data Group. - See sections 43.5.2 ( $m_{{T}}$ ) and 43.6.1 ( $M_{{T}}$ ) for definitions of transverse mass.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.