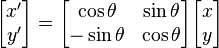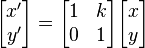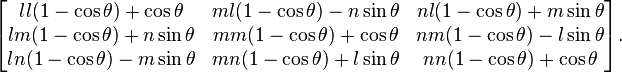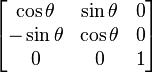Transformation matrix
In linear algebra, linear transformations can be represented by matrices. If T is a linear transformation mapping Rn to Rm and 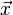 is a column vector with n entries, then
is a column vector with n entries, then
for some m×n matrix A, called the transformation matrix of T. There is an alternative expression of transformation matrices involving row vectors that is preferred by some authors.
Uses
Matrices allow arbitrary linear transformations to be represented in a consistent format, suitable for computation.[1] This also allows transformations to be concatenated easily (by multiplying their matrices).
Linear transformations are not the only ones that can be represented by matrices. Some transformations that are non-linear on a n-dimensional Euclidean space Rn, can be represented as linear transformations on the n+1-dimensional space Rn+1. These include both affine transformations (such as translation) and projective transformations. For this reason, 4×4 transformation matrices are widely used in 3D computer graphics. These n+1-dimensional transformation matrices are called, depending on their application, affine transformation matrices, projective transformation matrices, or more generally non-linear transformation matrices. With respect to an n-dimensional matrix, an n+1-dimensional matrix can be described as an augmented matrix.
In the physical sciences, an active transformation is one which actually changes the physical position of a system, and makes sense even in the absence of a coordinate system whereas a passive transformation is a change in the coordinate description of the physical system (change of basis). The distinction between active and passive transformations is important. By default, by transformation, mathematicians usually mean active transformations, while physicists could mean either.
Put differently, a passive transformation refers to observation of the same event from two different coordinate frames.
Finding the matrix of a transformation
If one has a linear transformation  in functional form, it is easy to determine the transformation matrix A by transforming each of the vectors of the standard basis by T, then inserting the result into the columns of a matrix. In other words,
in functional form, it is easy to determine the transformation matrix A by transforming each of the vectors of the standard basis by T, then inserting the result into the columns of a matrix. In other words,
For example, the function  is a linear transformation. Applying the above process (suppose that n = 2 in this case) reveals that
is a linear transformation. Applying the above process (suppose that n = 2 in this case) reveals that
It must be noted that the matrix representation of vectors and operators depends on the chosen basis; a similar matrix will result from an alternate basis. Nevertheless, the method to find the components remains the same.
To elaborate, vector v can be represented in basis vectors, ![E=[{\vec e}_{1}{\vec e}_{2}\ldots {\vec e}_{n}]](/2014-wikipedia_en_all_02_2014/I/media/9/0/0/2/900242a9366b1e9e6b301c7183d342d2.png) with coordinates
with coordinates ![[v]_{E}=[v_{1}v_{2}\ldots v_{n}]^{T}](/2014-wikipedia_en_all_02_2014/I/media/1/8/2/e/182efb6b09818678669f5a168be731b4.png) :
:
Now, express the result of the transformation matrix A upon 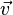 , in the given basis:
, in the given basis:
The 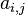 elements of matrix A are determined for a given basis E by applying A to every
elements of matrix A are determined for a given basis E by applying A to every ![{\vec e}_{j}=[00\ldots (v_{j}=1)\ldots 0]^{T}](/2014-wikipedia_en_all_02_2014/I/media/f/a/e/d/faed33037c9b073175e61eccddad1cd0.png) , and observing the response vector
, and observing the response vector  . This equation defines the wanted elements,
. This equation defines the wanted elements, 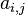 , of j-th column of the matrix A.[2]
, of j-th column of the matrix A.[2]
Eigenbasis and diagonal matrix
Yet, there is a special basis for an operator in which the components form a diagonal matrix and, thus, multiplication complexity reduces to n. Being diagonal means that all coefficients 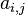 but
but 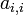 are zeros leaving only one term in the sum
are zeros leaving only one term in the sum  above. The surviving diagonal elements,
above. The surviving diagonal elements, 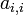 , are known as eigenvalues and designated with
, are known as eigenvalues and designated with 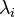 in the defining equation, which reduces to
in the defining equation, which reduces to 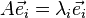 . The resulting equation is known as eigenvalue equation.[3] The eigenvectors and eigenvalues are derived from it via the characteristic polynomial.
. The resulting equation is known as eigenvalue equation.[3] The eigenvectors and eigenvalues are derived from it via the characteristic polynomial.
With diagonalization, it is often possible to translate to and from eigenbases.
Examples in 2D graphics
Most common geometric transformations that keep the origin fixed are linear, including rotation, scaling, shearing, reflection, and orthogonal projection; if an affine transformation is not a pure translation it keeps some point fixed, and that point can be chosen as origin to make the transformation linear. In two dimensions, linear transformations can be represented using a 2×2 transformation matrix.
Rotation
For rotation by an angle θ clockwise about the origin (Note that this definition of clockwise is dependent on the x axis pointing right and the y axis pointing up. In for example SVG, where the y axis points down, the below matrices must be swapped) the functional form is  and
and 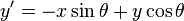 . Written in matrix form, this becomes:
. Written in matrix form, this becomes:
Similarly, for a rotation counter clockwise about the origin, the functional form is  and
and  and the matrix form is:
and the matrix form is:
Scaling
For scaling (that is, enlarging or shrinking), we have  and
and  . The matrix form is:
. The matrix form is:
When  , then the matrix is a squeeze mapping and preserves areas in the plane.
, then the matrix is a squeeze mapping and preserves areas in the plane.
If  or
or 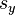 is greater than 1 in absolute value, the transformation stretches the figures in the corresponding direction; if less than 1, it shrinks them in that direction. Negative values of
is greater than 1 in absolute value, the transformation stretches the figures in the corresponding direction; if less than 1, it shrinks them in that direction. Negative values of  or
or 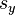 also flips (mirrors) the points in that direction.
also flips (mirrors) the points in that direction.
Applying this sort of scaling  times is equivalent to applying a single scaling with factors
times is equivalent to applying a single scaling with factors 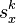 and
and  .
.
More generally, any symmetric 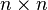 matrix defines a scaling along two perpendicular axes (the eigenvectors of the matrix) by equal or distinct factors (the eigenvalues corresponding to those eigenvectors).
matrix defines a scaling along two perpendicular axes (the eigenvectors of the matrix) by equal or distinct factors (the eigenvalues corresponding to those eigenvectors).
Shearing
For shear mapping (visually similar to slanting), there are two possibilities.
A shear parallel to the x axis has  and
and  . Written in matrix form, this becomes:
. Written in matrix form, this becomes:
A shear parallel to the y axis has  and
and  , which has matrix form:
, which has matrix form:
Reflection
To reflect a vector about a line that goes through the origin, let  be a vector in the direction of the line:
be a vector in the direction of the line:
Orthogonal projection
To project a vector orthogonally onto a line that goes through the origin, let  be a vector in the direction of the line. Then use the transformation matrix:
be a vector in the direction of the line. Then use the transformation matrix:
As with reflections, the orthogonal projection onto a line that does not pass through the origin is an affine, not linear, transformation.
Parallel projections are also linear transformations and can be represented simply by a matrix. However, perspective projections are not, and to represent these with a matrix, homogeneous coordinates must be used.
Examples in 3D graphics
Rotation
The matrix to rotate an angle θ about the axis defined by unit vector (l,m,n) is[4]
Reflection
To reflect a point through a plane  (which goes through the origin), one can use
(which goes through the origin), one can use 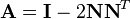 , where
, where  is the 3x3 identity matrix and
is the 3x3 identity matrix and  is the three-dimensional unit vector for the vector normal of the plane. If the L2 norm of
is the three-dimensional unit vector for the vector normal of the plane. If the L2 norm of  and
and  is unity, the transformation matrix can be expressed as:
is unity, the transformation matrix can be expressed as:
Note that these are particular cases of a Householder reflection in two and three dimensions. A reflection about a line or plane that does not go through the origin is not a linear transformation; it is an affine transformation.
Composing and inverting transformations
One of the main motivations for using matrices to represent linear transformations is that transformations can then be easily composed (combined) and inverted.
Composition is accomplished by matrix multiplication. If A and B are the matrices of two linear transformations, then the effect of applying first A and then B to a vector x is given by:
(This is called the associative property.) In other words, the matrix of the combined transformation A followed by B is simply the product of the individual matrices. Note that the multiplication is done in the opposite order from the English sentence: the matrix of "A followed by B" is BA, not AB.
A consequence of the ability to compose transformations by multiplying their matrices is that transformations can also be inverted by simply inverting their matrices. So, A−1 represents the transformation that "undoes" A.
Other kinds of transformations
Affine transformations
To represent affine transformations with matrices, we can use homogeneous coordinates. This means representing a 2-vector (x, y) as a 3-vector (x, y, 1), and similarly for higher dimensions. Using this system, translation can be expressed with matrix multiplication. The functional form  becomes:
becomes:
All ordinary linear transformations are included in the set of affine transformations, and can be described as a simplified form of affine transformations. Therefore, any linear transformation can be also represented by a general transformation matrix. The latter is obtained by expanding the corresponding linear transformation matrix by one row and column, filling the extra space with zeros except for the lower-right corner, which must be set to 1. For example, the clockwise rotation matrix from above becomes:
Using transformation matrices containing homogeneous coordinates, translations can be seamlessly intermixed with all other types of transformations. The reason is that the real plane is mapped to the w = 1 plane in real projective space, and so translation in real Euclidean space can be represented as a shear in real projective space. Although a translation is a non-linear transformation in a 2-D or 3-D Euclidean space described by Cartesian coordinates, it becomes, in a 3-D or 4-D projective space described by homogeneous coordinates, a simple linear transformation (a shear).
When using affine transformations, the homogeneous component of a coordinate vector (normally called w) will never be altered. One can therefore safely assume that it is always 1 and ignore it. However, this is not true when using perspective projections.
Perspective projection
Another type of transformation, of importance in 3D computer graphics, is the perspective projection. Whereas parallel projections are used to project points onto the image plane along parallel lines, the perspective projection projects points onto the image plane along lines that emanate from a single point, called the center of projection. This means that an object has a smaller projection when it is far away from the center of projection and a larger projection when it is closer.
The simplest perspective projection uses the origin as the center of projection, and z = 1 as the image plane. The functional form of this transformation is then 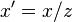 ;
;  . We can express this in homogeneous coordinates as:
. We can express this in homogeneous coordinates as:
After carrying out the matrix multiplication, the homogeneous component wc will, in general, not be equal to 1. Therefore, to map back into the real plane we must perform the homogeneous divide or perspective divide by dividing each component by wc:
More complicated perspective projections can be composed by combining this one with rotations, scales, translations, and shears to move the image plane and center of projection wherever they are desired.
See also
References
- ↑ Gentle, James E. (2007). "Matrix Transformations and Factorizations". Matrix Algebra: Theory, Computations, and Applications in Statistics. Springer. ISBN 9780387708737.
- ↑ Nearing, James (2010). "Chapter 7.3 Examples of Operators". Mathematical Tools for Physics. ISBN 048648212X. Retrieved January 1, 2012.
- ↑ Nearing, James (2010). "Chapter 7.9: Eigenvalues and Eigenvectors". Mathematical Tools for Physics. ISBN 048648212X. Retrieved January 1, 2012.
- ↑ Szymanski, John E. (1989). Basic Mathematics for Electronic Engineers:Models and Applications. Taylor & Francis. p. 154. ISBN 0278000681.
External links
- The Matrix Page Practical examples in POV-Ray
- Reference page - Rotation of axes
- Linear Transformation Calculator
- Transformation Applet - Generate matrices from 2D transformations and vice versa.



![{\vec v}=v_{1}{\vec e}_{1}+v_{2}{\vec e}_{2}+\ldots +v_{n}{\vec e}_{n}=\sum v_{i}{\vec e}_{i}=E[v]_{E}](/2014-wikipedia_en_all_02_2014/I/media/c/b/7/d/cb7d6c9416280c442b8aea1ffedd1756.png)
![A({\vec v})=A(\sum {v_{i}{\vec e}_{i}})=\sum {v_{i}A({\vec e}_{i})}=[A({\vec e}_{1})A({\vec e}_{2})\ldots A({\vec e}_{n})][v]_{E}=](/2014-wikipedia_en_all_02_2014/I/media/9/3/e/2/93e26fd8c1b630687947d935805e292d.png)
![\;=\;A\cdot [v]_{E}=[{\vec e}_{1}{\vec e}_{2}\ldots {\vec e}_{n}]{\begin{bmatrix}a_{{1,1}}&a_{{1,2}}&\ldots &a_{{1,n}}\\a_{{2,1}}&a_{{2,2}}&\ldots &a_{{2,n}}\\\vdots &\vdots &\ddots &\vdots \\a_{{n,1}}&a_{{n,2}}&\ldots &a_{{n,n}}\\\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\\\vdots \\v_{n}\end{bmatrix}}](/2014-wikipedia_en_all_02_2014/I/media/8/2/0/d/820d4a05ffd2b9204a90604482604cc4.png)