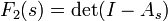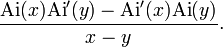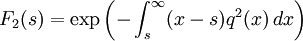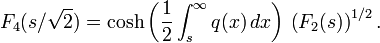Tracy–Widom distribution
The Tracy–Widom distribution, introduced by Craig Tracy and Harold Widom (1993, 1994), is the probability distribution of the largest eigenvalue of a random hermitian matrix in the edge scaling limit. It also appears in the distribution of the length of the longest increasing subsequence of random permutations (Baik, Deift & Johansson 1999) and in current fluctuations of the asymmetric simple exclusion process (ASEP) with step initial condition (Johansson 2000, Tracy & Widom 2009). See (Takeuchi & Sano 2010, Takeuchi et al. 2011) for experimental testing (and verifying) that the interface fluctuations of a growing droplet (or substrate) are described by the TW distribution  (or
(or 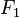 ) as predicted by (Prähofer & Spohn 2000).
) as predicted by (Prähofer & Spohn 2000).
The cumulative distribution function of the Tracy–Widom distribution can be given as the Fredholm determinant
of the operator As on square integrable function on the half line (s, ∞) with kernel given in terms of Airy functions Ai by
It can also be given as an integral
in terms of a solution of a Painlevé equation of type II
where q, called the Hastings-McLeod solution, satisfies the boundary condition
The distribution F2 is associated to unitary ensembles in random matrix theory. There are analogous Tracy–Widom distributions F1 and F4 for orthogonal (β=1) and symplectic ensembles (β=4) that are also expressible in terms of the same Painlevé transcendent q (Tracy & Widom 1996):
and
The distribution F1 is of particular interest in multivariate statistics (Johnstone 2007, 2008, 2009). For a discussion of the universality of Fβ, β=1,2, and 4, see Deift (2007). For an application of F1 to inferring population structure from genetic data see Patterson, Price & Reich (2006).
Numerical techniques for obtaining numerical solutions to the Painlevé equations of the types II and V, and numerically evaluating eigenvalue distributions of random matrices in the beta-ensembles were first presented by Edelman & Persson (2005) using MATLAB. These approximation techniques were further analytically justified in Bejan (2005) and used to provide numerical evaluation of Painlevé II and Tracy–Widom distributions (for β=1,2, and 4) in S-PLUS. These distributions have been tabulated in Bejan (2005) to four significant digits for values of the argument in increments of 0.01; a statistical table for p-values was also given in this work. Bornemann (2009) gave accurate and fast algorithms for the numerical evaluation of Fβ and the density functions fβ(s)=dFβ/ds for β=1,2, and 4. These algorithms can be used to compute numerically the mean, variance, skewness and kurtosis of the distributions Fβ.
| β | Mean | Variance | Skewness | Kurtosis |
|---|---|---|---|---|
| 1 | -1.2065335745820 | 1.607781034581 | 0.29346452408 | 0.1652429384 |
| 2 | -1.771086807411 | 0.8131947928329 | 0.224084203610 | 0.0934480876 |
| 4 | -2.306884893241 | 0.5177237207726 | 0.16550949435 | 0.0491951565 |
Functions for working with the Tracy-Widom laws are also presented in the R package 'RMTstat' by Johnstone et al. (2009) and MATLAB package 'RMLab' by Dieng (2006).
For an extension of the definition of the Tracy–Widom distributions Fβ to all β>0 see Ramírez, Rider & Virág (2006).
For a simple approximation based on a shifted gamma distribution see Chiani (2012).
References
- Baik, J.; Deift, P.; Johansson, K. (1999), "On the distribution of the length of the longest increasing subsequence of random permutations", Journal of the American Mathematical Society 12 (4): 1119–1178, doi:10.1090/S0894-0347-99-00307-0, JSTOR 2646100, MR 1682248.
- Deift, P. (2007), "Universality for mathematical and physical systems", International Congress of Mathematicians (Madrid, 2006), European Mathematical Society, pp. 125–152, MR 2334189.
- Johansson, K. (2000), "Shape fluctuations and random matrices", Communications in Mathematical Physics 209 (2): 437–476, arXiv:math/9903134, Bibcode:2000CMaPh.209..437J, doi:10.1007/s002200050027.
- Johansson, K. (2002), "Toeplitz determinants, random growth and determinantal processes", Proc. International Congress of Mathematicians (Beijing, 2002) 3, Beijing: Higher Ed. Press, pp. 53–62, MR 1957518.
- Johnstone, I. M. (2007), "High dimensional statistical inference and random matrices", International Congress of Mathematicians (Madrid, 2006), European Mathematical Society, pp. 307–333, MR 2334195.
- Johnstone, I. M. (2008), "Multivariate analysis and Jacobi ensembles: largest eigenvalue, Tracy-Widom limits and rates of convergence", Annals of Statistics 36 (6): 2638–2716, arXiv:0803.3408, doi:10.1214/08-AOS605, PMC 2821031, PMID 20157626.
- Johnstone, I. M. (2009), "Approximate null distribution of the largest root in multivariate analysis", Annals of Applied Statistics 3 (4): 1616–1633, arXiv:1009.5854, doi:10.1214/08-AOAS220, PMC 2880335, PMID 20526465.
- Patterson, N.; Price, A. L.; Reich, D. (2006), "Population structure and eigenanalysis", PLoS Genetics 2 (12): e190, doi:10.1371/journal.pgen.0020190, PMC 1713260, PMID 17194218.
- Prähofer, M.; Spohn, H. (2000), "Universal distributions for growing processes in 1+1 dimensions and random matrices", Physical Review Letters 84 (21): 4882–4885, arXiv:cond-mat/9912264, Bibcode:2000PhRvL..84.4882P, doi:10.1103/PhysRevLett.84.4882, PMID 10990822.
- Takeuchi, K. A.; Sano, M. (2010), "Universal fluctuations of growing interfaces: Evidence in turbulent liquid crystals", Physical Review Letters 104 (23): 230601, arXiv:1001.5121, Bibcode:2010PhRvL.104w0601T, doi:10.1103/PhysRevLett.104.230601, PMID 20867221
- Takeuchi, K. A.; Sano, M.; Sasamoto, T.; Spohn, H. (2011), "Growing interfaces uncover universal fluctuations behind scale invariance", Scientific Reports 1: 34, arXiv:1108.2118, Bibcode:2011NatSR...1E..34T, doi:10.1038/srep00034
- Tracy, C. A.; Widom, H. (1993), "Level-spacing distributions and the Airy kernel", Physics Letters B 305 (1-2): 115–118, arXiv:hep-th/9210074, Bibcode:1993PhLB..305..115T, doi:10.1016/0370-2693(93)91114-3.
- Tracy, C. A.; Widom, H. (1994), "Level-spacing distributions and the Airy kernel", Communications in Mathematical Physics 159 (1): 151–174, arXiv:hep-th/9211141, Bibcode:1994CMaPh.159..151T, doi:10.1007/BF02100489, MR 1257246.
- Tracy, C. A.; Widom, H. (1996), "On orthogonal and symplectic matrix ensembles", Communications in Mathematical Physics 177 (3): 727–754, Bibcode:1996CMaPh.177..727T, doi:10.1007/BF02099545, MR 1385083.
- Tracy, C. A.; Widom, H. (2002), "Distribution functions for largest eigenvalues and their applications", Proc. International Congress of Mathematicians (Beijing, 2002) 1, Beijing: Higher Ed. Press, pp. 587–596, MR 1989209.
- Tracy, C. A.; Widom, H. (2009), "Asymptotics in ASEP with step initial condition", Communications in Mathematical Physics 290 (1): 129–154, arXiv:0807.1713, Bibcode:2009CMaPh.290..129T, doi:10.1007/s00220-009-0761-0.
Additional reading
- Bejan, Andrei Iu. (2005), Largest eigenvalues and sample covariance matrices. Tracy-Widom and Painleve II: Computational aspects and realization in S-Plus with applications, M.Sc. dissertation, Department of Statistics, The University of Warwick.
- Bornemann, F. (2010), "On the numerical evaluation of distributions in random matrix theory: A review with an invitation to experimental mathematics", Markov Processes and Related Fields 16 (4): 803–866, arXiv:0904.1581, Bibcode:2009arXiv0904.1581B.
- Chiani, M. (2012), Distribution of the largest eigenvalue for real Wishart and Gaussian random matrices and a simple approximation for the Tracy-Widom distribution, arXiv:1209.3394.
- Edelman, A.; Persson, P.-O. (2005), Numerical Methods for Eigenvalue Distributions of Random Matrices, arXiv:math-ph/0501068, Bibcode:2005math.ph...1068E.
- Ramírez, J. A.; Rider, B.; Virág, B. (2006), Beta ensembles, stochastic Airy spectrum, and a diffusion, arXiv:math/0607331, Bibcode:2006math......7331R.
External links
- Kuijlaars, Universality of distribution functions in random matrix theory.
- Tracy, C. A.; Widom, H., The distributions of random matrix theory and their applications.
- Johnstone, Iain; Ma, Zongming; Perry, Patrick; Shahram, Morteza (2009), Package 'RMTstat'.
- Dieng, Momar (2006), Package ``RMLab.