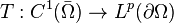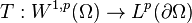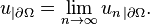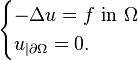Trace operator

From Wikipedia, the free encyclopedia

A function defined on a rectangle (top figure, in red), and its trace (bottom figure, in red).

In mathematics, the concept of trace operator plays an important role in studying the existence and uniqueness of solutions to boundary value problems, that is, to partial differential equations with prescribed boundary conditions. The trace operator makes it possible to extend the notion of restriction of a function to the boundary of its domain to "generalized" functions in a Sobolev space.

Informal discussion

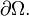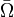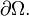Let $\Omega$ be a bounded open set in the Euclidean space ${\mathbb R}^{n}$ with C¹ boundary $\partial \Omega .$ If $u$ is a function that is $C^{1}$ (or even just continuous) on the closure ${\bar \Omega }$ of $\Omega ,$ its function restriction is well-defined and continuous on $\partial \Omega .$ If however, $u$ is the solution to some partial differential equation, it is in general a weak solution, so it belongs to some Sobolev space. 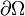Such functions are defined only up to a set of measure zero, and since the boundary $\partial \Omega$ does have measure zero, any function in a Sobolev space can be completely redefined on the boundary without changing the function as an element in that space. It follows that simple function restriction cannot be used to meaningfully define what it means for a general solution to a partial differential equation to behave in a prescribed way on the boundary of $\Omega .$

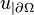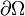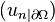The way out of this difficulty is the observation that while an element $u$ in a Sobolev space may be ill-defined as a function, $u$ can be nevertheless approximated by a sequence $(u_{n})$ of $C^{1}$ functions defined on the closure of $\Omega .$ Then, the restriction $u_{{|\partial \Omega }}$ of $u$ to $\partial \Omega$ is defined as the limit of the sequence of restrictions $(u_{{n|\partial \Omega }})$ .

Construction of the trace operator

To rigorously define the notion of restriction to a function in a Sobolev space, let $p\geq 1$ be a real number. Consider the linear operator

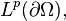$T:C^{1}({\bar \Omega })\to L^{p}(\partial \Omega )$

defined on the set of all $C^{1}$ functions on the closure of $\Omega$ with values in the Lp space $L^{p}(\partial \Omega ),$ given by the formula

$Tu=u_{{|\partial \Omega }}.\,$

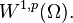The domain of $T$ is a subset of the Sobolev space $W^{{1,p}}(\Omega ).$ It can be proved that there exists a constant $C$ depending only on $\Omega$ and $p,$ such that

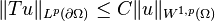$\|Tu\|_{{L^{{p}}(\partial \Omega )}}\leq C\|u\|_{{W^{{1,p}}(\Omega )}}$ for all $u$ in $C^{1}({\bar \Omega }).$

Then, since the $C^{1}$ functions on ${\bar \Omega }$ are dense in $W^{{1,p}}(\Omega )$ , the operator $T$ admits a continuous extension

$T:W^{{1,p}}(\Omega )\to L^{p}(\partial \Omega )\,$

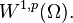
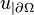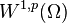defined on the entire space $W^{{1,p}}(\Omega ).$ $T$ is called the trace operator. The restriction (or trace) $u_{{|\partial \Omega }}$ of a function $u$ in $W^{{1,p}}(\Omega )$ is then defined as $Tu.$

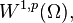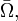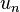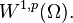This argument can be made more concrete as follows. Given a function $u$ in $W^{{1,p}}(\Omega ),$ consider a sequence of functions $(u_{n})$ that are $C^{1}$ on ${\bar \Omega },$ with $u_{n}$ converging to $u$ in the norm of $W^{{1,p}}(\Omega ).$ Then, by the above inequality, the sequence 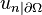$u_{{n|\partial \Omega }}$ will be convergent in 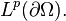$L^{p}(\partial \Omega ).$ Define

$u_{{|\partial \Omega }}=\lim _{{n\to \infty }}u_{{n\,|\partial \Omega }}.\,$

It can be shown that this definition is independent of the sequence $(u_{n})$ approximating $u.$

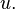
Application

Consider the problem of solving Poisson's equation with zero boundary conditions:

${\begin{cases}-\Delta u=f{\text{ in }}\Omega \\u_{{|\partial \Omega }}=0.\end{cases}}$

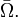
Here, $f$ is a given continuous function on ${\bar \Omega }.$

With the help of the concept of trace, define the subspace 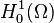$H_{0}^{1}(\Omega )$ to be all functions in the Sobolev space $W^{{1,2}}(\Omega )$ (this space is also denoted $H^{1}(\Omega )$ ) whose trace is zero. Then, the equation above can be given the weak formulation

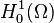Find $u$ in $H_{0}^{1}(\Omega )$ such that

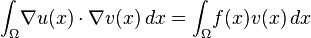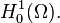
$\int _{\Omega }\!\nabla u(x)\cdot \nabla v(x)\,dx=\int _{\Omega }\!f(x)v(x)\,dx$ for all $v$ in $H_{0}^{1}(\Omega ).$

Using the Lax–Milgram theorem one can then prove that this equation has precisely one solution, which implies that the original equation has precisely one weak solution.

One can employ similar ideas to prove the existence and uniqueness of more complicated partial differential equations and with other boundary conditions (such as Neumann and Robin), with the notion of trace playing an important role in all such problems.

References

Evans, Lawrence (1998). Partial differential equations. Providence, R.I.: American Mathematical Society. pp. 257–261. ISBN 0-8218-0772-2.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.