Townsend discharge
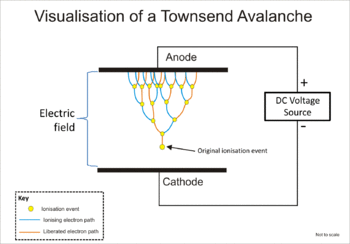
The Townsend discharge is a gas ionization process where free electrons, accelerated by a sufficiently strong electric field, give rise to electrical conduction through a gas by avalanche multiplication caused by the ionization of molecules by ion impact. When the number of free charges drops or the electric field weakens, the phenomenon ceases.
The Townsend discharge is named after John Sealy Townsend, who discovered the fundamental ionization mechanism by his work between 1897 and 1901. It is also known as a "Townsend avalanche".
General description of the phenomenon
The avalanche is a cascade reaction involving electrons in a region with a sufficiently high electric field in a gaseous medium that can be ionized, such as air. Following an original ionisation event, due to such as ionising radiation, the positive ion drifts towards the cathode, while the free electron drifts towards the anode of the device. If the electric field is strong enough, the free electron gains sufficient energy to liberate a further electron when it next collides with another molecule. The two free electrons then travel towards the anode and gain sufficient energy from the electric field to cause impact ionisation when the next collisions occur; and so on. This is effectively a chain reaction of electron generation, and is dependent on the free electrons gaining sufficient energy between collisions to sustain the avalanche.[1] The total number of electrons reaching the anode is equal to the number of collisions, plus the single initiating free electron. The limit to the multiplication in an electron avalanche is known as the Raether limit.
The Townsend avalanche can have a large range of current densities. In common gas filled tubes, such as those used as gaseous ionization detectors, magnitudes of currents flowing during this process can range from about 10−18 amperes to about 10−5 amperes.[citation needed] Any subsequent transitions to the ionisation processes of dark discharge, glow discharge, and finally to arc discharge are driven by increasing current densities. However in all these discharge regimes, the basic mechanism of conduction is avalanche breakdown.
Quantitative description of the phenomenon
The basic setup of Townsend's early experiments investigating ionization discharges in gases consisted of planar parallel plates forming two sides of a chamber filled with a gas. A high voltage direct current voltage source was connected between the plates, the lower voltage plate being the cathode while the other was the anode. Forcing the cathode to emit electrons by the photoelectric effect, by irradiating it for example with an X-ray source, Townsend found that the current  flowing through the chamber depends on the electric field between the plates in such a way that gas ions seemed to multiply as they moved between them. He observed currents varying exponentially over ten or more orders of magnitude with a constant applied voltage when the distance between the plates was varied. He also discovered the importance of the pressure of the gaseous medium, and was able to generate ions in gases at low pressure with a much lower voltage than that required to generate a spark. This overturned conventional thinking about the amount of current that an irradiated gas could conduct.[2]
flowing through the chamber depends on the electric field between the plates in such a way that gas ions seemed to multiply as they moved between them. He observed currents varying exponentially over ten or more orders of magnitude with a constant applied voltage when the distance between the plates was varied. He also discovered the importance of the pressure of the gaseous medium, and was able to generate ions in gases at low pressure with a much lower voltage than that required to generate a spark. This overturned conventional thinking about the amount of current that an irradiated gas could conduct.[2]
The experimental data obtained from his experiments are described by the following formula
where
 is the current flowing in the device,
is the current flowing in the device, is the photoelectric current generated at the cathode surface,
is the photoelectric current generated at the cathode surface, is the Euler number
is the Euler number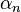 is the first Townsend ionization coefficient, expressing the number of ion pairs generated per unit length (e.g. meter) by a negative ion (anion) moving from cathode to anode,
is the first Townsend ionization coefficient, expressing the number of ion pairs generated per unit length (e.g. meter) by a negative ion (anion) moving from cathode to anode, is the distance between the plates of the device.
is the distance between the plates of the device.
The almost constant voltage between the plates is equal to the breakdown voltage needed to create a self-sustaining avalanche: it decreases when the current reaches the glow discharge regime. Subsequent experiments revealed that the current  rises faster than predicted by the above formula as the distance
rises faster than predicted by the above formula as the distance  increases: two different effects were considered in order to explain the physics of the phenomenon and to be able to do a precise quantitative calculation.
increases: two different effects were considered in order to explain the physics of the phenomenon and to be able to do a precise quantitative calculation.
Gas ionization caused by motion of positive ions
Townsend put forward the hypothesis that positive ions also produce ion pairs, introducing a coefficient 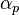 expressing the number of ion pairs generated per unit length by a positive ion (cation) moving from anode to cathode. The following formula was found
expressing the number of ion pairs generated per unit length by a positive ion (cation) moving from anode to cathode. The following formula was found
since  , in very good agreement with experiments.
, in very good agreement with experiments.
The first Townsend coefficient ( α ), also known as first Townsend avalanche coefficient is a term used where secondary ionization occurs because the primary ionization electrons gain sufficient energy from the accelerating electric field, or from the original ionizing particle. The coefficient gives the number of secondary electrons produced by primary electron per unit path length.
Cathode emission caused by impact of ions
Townsend, Holst and Oosterhuis also put forward an alternative hypothesis, considering the augmented emission of electrons by the cathode caused by impact of positive ions. This introduced Townsend's second ionization coefficient  ; the average number of electrons released from a surface by an incident positive ion, according to the following formula:
; the average number of electrons released from a surface by an incident positive ion, according to the following formula:
These two formulas may be thought as describing limiting cases of the effective behavior of the process: note that either can be used to describe the same experimental results. Other formulas describing various intermediate behaviors are found in the literature, particularly in reference 1 and citations therein.
Conditions

A: random pulses by cosmic radiation
B: saturation current
C: avalanche Townsend discharge
D: self-sustained Townsend discharge
E: unstable region: corona discharge
F: sub-normal glow discharge
G: normal glow discharge
H: abnormal glow discharge
I: unstable region: glow-arc transition
J: electric arc
K: electric arc
A-D region: dark discharge; ionization occurs, current below 10 microamps.
F-H region: glow discharge; the plasma emits a faint glow.
I-K region: arc discharge; larges amounts of radiation produced.
A Townsend discharge can be sustained only over a limited range of gas pressure and electric field intensity. The accompanying plot shows the variation of voltage drop and the different operating regions for a gas-filled tube with a constant pressure, but a varying current between its electrodes. The Townsend avalanche phenomena occurs on the sloping plateau B-D. Beyond D the ionisation is sustained.
At higher pressures, discharges occur more rapidly than the calculated time for ions to traverse the gap between electrodes, and the streamer theory of spark discharge of Raether, Meek and Loeb is applicable. In highly non-uniform electric fields, the corona discharge process is applicable. See Electron avalanche for further description of these mechanisms.
Discharges in vacuum require vaporization and ionization of electrode atoms. An arc can be initiated without a preliminary Townsend discharge; for example when electrodes touch and are then separated.
Applications
Gas-discharge tubes
The starting of Townsend discharge sets the upper limit to the blocking voltage a glow discharge gas filled tube can withstand this limit is the Townsend discharge breakdown voltage also called ignition voltage of the tube.

The occurrence of Townsend discharge, leading to glow discharge breakdown shapes the current-voltage characteristic of a gas discharge tube such as a neon lamp in a way such that it has a negative differential resistance region of the S-type. The negative resistance can be used to generate electrical oscillations and waveforms, as in the relaxation oscillator whose schematic is shown in the picture on the right. The sawtooth shaped oscillation generated has frequency
- where
 is the glow discharge breakdown voltage,
is the glow discharge breakdown voltage, is the Townsend discharge breakdown voltage,
is the Townsend discharge breakdown voltage,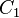 ,
, 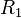 and
and 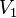 are respectively the capacitance, the resistance and the supply voltage of the circuit.
are respectively the capacitance, the resistance and the supply voltage of the circuit.
- Since temperature and time stability of the characteristics of gas diodes and neon lamps is low, and also the statistical dispersion of breakdown voltages is high, the above formula can only give a qualitative indication of what the real frequency of oscillation is.
Gas phototubes
Avalanche multiplication during Townsend discharge is naturally used in gas phototubes, to amplify the photoelectric charge generated by incident radiation (visible light or not) on the cathode: achievable current is typically 10~20 times greater respect to that generated by vacuum phototubes.
Ionising radiation detectors

Townsend avalanche discharges are fundamental to the operation of gaseous ionization detectors such as the Geiger–Müller tube and the Proportional counter in either detecting ionizing radiation or measuring its energy. The incident radiation will ionise atoms or molecules in the gaseous medium to produce ion pairs, but different use is made by each detector type of the resultant avalanche effects.
In the case of a GM tube the high electric field strength is sufficient to cause complete ionisation of the fill gas surrounding the anode from the initial creation of just one ion pair. The GM tube output carries information that the event has occurred, but no information about the energy of the incident radiation.[1]
In the case of proportional counters, multiple creation of ion pairs occurs in the "ion drift" region near the cathode. The electric field and chamber geometries are selected so that an "avalanche region" is created in the immediate proximity of the anode. A negative ion drifting towards the anode enters this region and creates a localised avalanche that is independent of those from other ion pairs, but which can still provide a multiplication effect. In this way spectroscopic information on the energy of the incident radiation is available by the magnitude of the output pulse from each initiating event.[1]
The accompanying plot shows the variation of ionisation current for a co-axial cylinder system. In the ion chamber region, there are no avalanches and the applied voltage only serves to move the ions towards the electrodes to prevent re-combination. In the proportional region, localised avalanches occur in the gas space immediately round the anode. Increasing the voltage increases the number of avalanches and thereby current, until the Geiger region is reached where the full volume of the fill gas around the anodes ionised, and all energy information is lost.[1] Beyond the Geiger region the gas is in continuous discharge owing to the high electric field strength.
See also
- Avalanche breakdown
- Electric arc
- Electric discharge in gases
- Field electron emission
- Paschen's law
- Photoelectric effect
- Townsend (unit)
References
- Little, P.F. (1956). "Secondary effects". In Flügge, Siegfried. Electron-emission • Gas discharges I. Handbuch der Physik (Encyclopedia of Physics) XXI. Berlin-Heidelberg-New York: Springer-Verlag. pp. 574–663..
- James W Gewartowski and Hugh Alexander Watson (1965). Principles of Electron Tubes: Including Grid-controlled Tubes, Microwave Tubes and Gas Tubes. D. Van Nostrand Co, Inc.
- Herbert J. Reich (1939, 1944). Theory and applications of electron tubes. McGraw-Hill Co, Inc. Chapter 11 "Electrical conduction in gases" and chapter 12 "Glow- and Arc-discharge tubes and circuits".
- E.Kuffel, W.S. Zaengl, J.Kuffel (2004). High Voltage Engineering Fundamentals, Second edition. Butterworth-Heinemann. ISBN 0-7506-3634-3.
External links
- http://plasma.szfki.kfki.hu/~zoli/research/avalanche/ – simulation showing electron paths during avalanche



