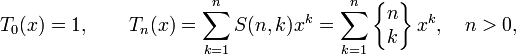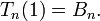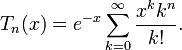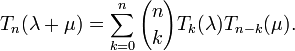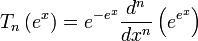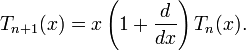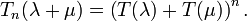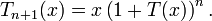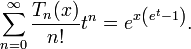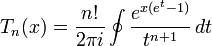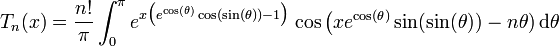Touchard polynomials

From Wikipedia, the free encyclopedia

For a different family of polynomials Q_n occasionally called Touchard polynomials, see Bateman polynomials.

The Touchard polynomials, studied by Jacques Touchard (1939), also called the exponential polynomials in ^[1]^[2] ,^[3] comprise a polynomial sequence of binomial type defined by

$T_{0}(x)=1,\qquad T_{n}(x)=\sum _{{k=1}}^{n}S(n,k)x^{k}=\sum _{{k=1}}^{n}\left\{{\begin{matrix}n\\k\end{matrix}}\right\}x^{k},\quad n>0,$

where S(n, k) is a Stirling number of the second kind, i.e., it is the number of partitions of a set of size n into k disjoint non-empty subsets. (The second notation above, with { braces }, was introduced by Donald Knuth.) The value at 1 of the nth Touchard polynomial is the nth Bell number, i.e., the number of partitions of a set of size n:

$T_{n}(1)=B_{n}.$

If X is a random variable with a Poisson distribution with expected value λ, then its nth moment is E(Xⁿ) = T_n(λ), leading to the definition:

$T_{{n}}(x)=e^{{-x}}\sum _{{k=0}}^{\infty }{\frac {x^{k}k^{n}}{k!}}.$

Using this fact one can quickly prove that this polynomial sequence is of binomial type, i.e., it satisfies the sequence of identities:

$T_{n}(\lambda +\mu )=\sum _{{k=0}}^{n}{n \choose k}T_{k}(\lambda )T_{{n-k}}(\mu ).$

The Touchard polynomials make up the only polynomial sequence of binomial type in which the coefficient of the 1st-degree term of every polynomial is 1.

$T_{{n+1}}(x)=x\sum _{{k=0}}^{n}{n \choose k}T_{k}(x).$

The Touchard polynomials satisfy the Rodrigues-like formula:

$T_{n}\left(e^{x}\right)=e^{{-e^{x}}}{\frac {d^{n}}{dx^{n}}}\left(e^{{e^{x}}}\right)$

The Touchard polynomials satisfy the recurrence relation

$T_{{n+1}}(x)=x\left(1+{\frac {d}{dx}}\right)T_{{n}}(x).$

And

$T_{{n+1}}(x)=x\sum _{{k=0}}^{n}{n \choose k}T_{k}(x).$

In case x = 1, this reduces to the recurrence formula for the Bell numbers.

Using the Umbral notation Tⁿ(x)=T_n(x),these formulas become:

$T_{n}(\lambda +\mu )=\left(T(\lambda )+T(\mu )\right)^{n}.$

$T_{{n+1}}(x)=x\left(1+T(x)\right)^{n}.$

The generating function of the Touchard polynomials is

$\sum _{{n=0}}^{\infty }{T_{n}(x) \over n!}t^{n}=e^{{x\left(e^{t}-1\right)}}.$

This corresponds to the generating function of Stirling numbers of the second kind#Generating function and ^[1] where it is referred to as Exponential Polynomials. And a contour-integral representation is

$T_{n}(x)={\frac {n!}{2\pi i}}\oint {\frac {e^{{x({e^{t}}-1)}}}{t^{{n+1}}}}\,dt$

The Touchard polynomials (and thereby the Bell numbers) can be generalized, using the real part of the above integral, to non-integer order:

$T_{n}(x)={\frac {n!}{\pi }}\int _{0}^{{\pi }}e^{{x{\bigl (}e^{{\cos(\theta )}}\cos(\sin(\theta ))-1{\bigr )}}}\cos {\bigl (}xe^{{\cos(\theta )}}\sin(\sin(\theta ))-n\theta )\,{\mathrm {d}}\theta$

References

↑ 1.0 1.1 Roman, Steven (1984). The Umbral Calculus. Dover. ISBN 0-486-44139-3.
↑ Boyadzhiev, Khristo N. "Exponential polynomials, Stirling numbers, and evaluation of some gamma integrals.". arxiv. Retrieved 23 November 2013.
↑ Brendt, Bruce C. "RAMANUJAN REACHES HIS HAND FROM HIS GRAVE TO SNATCH YOUR THEOREMS FROM YOU". Retrieved 23 November 2013.

Touchard, Jacques (1939), "Sur les cycles des substitutions", Acta Mathematica 70 (1): 243–297, doi:10.1007/BF02547349, ISSN 0001-5962, MR 1555449

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.