Totally disconnected space

From Wikipedia, the free encyclopedia

In topology and related branches of mathematics, a totally disconnected space is a topological space that is maximally disconnected, in the sense that it has no non-trivial connected subsets. In every topological space the empty set and the one-point sets are connected; in a totally disconnected space these are the only connected subsets.

An important example of a totally disconnected space is the Cantor set. Another example, playing a key role in algebraic number theory, is the field Q_p of p-adic numbers.

Definition

A topological space X is totally disconnected if the connected components in X are the one-point sets.

Examples

The following are examples of totally disconnected spaces:

Discrete spaces
The rational numbers
The irrational numbers
The p-adic numbers; more generally, profinite groups are totally disconnected.
The Cantor set
The Baire space
The Sorgenfrey line
Zero dimensional T₁ spaces
Extremally disconnected Hausdorff spaces
Stone spaces
The Knaster–Kuratowski fan provides an example of a connected space, such that the removal of a single point produces a totally disconnected space.
The Erdős space ℓ^p(Z)∩ 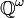${\mathbb {Q}}^{{\omega }}$ is a totally disconnected space that does not have dimension zero.

Properties

Subspaces, products, and coproducts of totally disconnected spaces are totally disconnected.
Totally disconnected spaces are T₁ spaces, since points are closed.
Continuous images of totally disconnected spaces are not necessarily totally disconnected, in fact, every compact metric space is a continuous image of the Cantor set.
A locally compact hausdorff space is zero-dimensional if and only if it is totally disconnected.
Every totally disconnected compact metric space is homeomorphic to a subset of a countable product of discrete spaces.
It is in general not true that every open set is also closed.
It is in general not true that the closure of every open set is open, i.e. not every totally disconnected Hausdorff space is extremally disconnected.

Constructing a disconnected space

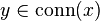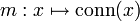Let $X$ be an arbitrary topological space. Let $x\sim y$ if and only if $y\in {\mathrm {conn}}(x)$ (where ${\mathrm {conn}}(x)$ denotes the largest connected subset containing $x$ ). This is obviously an equivalence relation. Endow $X/{\sim }$ with the quotient topology, i.e. the coarsest topology making the map $m:x\mapsto {\mathrm {conn}}(x)$ continuous. With a little bit of effort we can see that $X/{\sim }$ is totally disconnected. 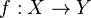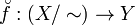We also have the following universal property: if $f:X\rightarrow Y$ a continuous map to a totally disconnected space, then it uniquely factors into $f={\breve {f}}\circ m$ where ${\breve {f}}:(X/\sim )\rightarrow Y$ is continuous.