Total quotient ring
In abstract algebra, the total quotient ring,[1] or total ring of fractions,[2] is a construction that generalizes the notion of the field of fractions of an integral domain to commutative rings R that may have zero divisors. The construction embeds R in a larger ring, giving every non-zero-divisor of R an inverse in the larger ring. Nothing more in A can be given an inverse, if one wants the homomorphism from A to the new ring to be injective.
Definition
Let  be a commutative ring and let
be a commutative ring and let 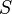 be the set of elements which are not zero divisors in
be the set of elements which are not zero divisors in  ; then
; then 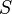 is a multiplicatively closed set. Hence we may localize the ring
is a multiplicatively closed set. Hence we may localize the ring  at the set
at the set 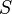 to obtain the total quotient ring
to obtain the total quotient ring  .
.
If  is a domain, then
is a domain, then  and the total quotient ring is the same as the field of fractions. This justifies the notation
and the total quotient ring is the same as the field of fractions. This justifies the notation  , which is sometimes used for the field of fractions as well, since there is no ambiguity in the case of a domain.
, which is sometimes used for the field of fractions as well, since there is no ambiguity in the case of a domain.
Since 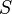 in the construction contains no zero divisors, the natural map
in the construction contains no zero divisors, the natural map 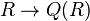 is injective, so the total quotient ring is an extension of
is injective, so the total quotient ring is an extension of  .
.
Examples
The total quotient ring 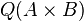 of a product ring is the product of total quotient rings
of a product ring is the product of total quotient rings  . In particular, if A and B are integral domains, it is the product of quotient fields.
. In particular, if A and B are integral domains, it is the product of quotient fields.
The total quotient ring of the ring of holomorphic functions on an open set D of complex numbers is the ring of meromorphic functions on D, even if D is not connected.
In an Artinian ring, all elements are units or zero divisors. Hence the set of non-zero divisors is the group of units of the ring,  , and so
, and so 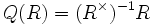 . But since all these elements already have inverses,
. But since all these elements already have inverses, 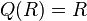 .
.
The same thing happens in a commutative von Neumann regular ring R. Suppose a in R is not a zero divisor. Then in a von Neumann regular ring a=axa for some x in R, giving the equation a(xa-1)=0. Since a is not a zero divisor, xa=1, showing a is a unit. Here again, 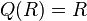 .
.
Applications
- The rational functions over a ring R can be constructed from the polynomial ring R[x] as a total quotient ring.[3]
- In algebraic geometry one considers a sheaf of total quotient rings on a scheme, and this may be used to give one possible definition of a Cartier divisor.
Generalization
If  is a commutative ring and
is a commutative ring and 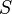 is any multiplicative subset in
is any multiplicative subset in  , the localization
, the localization  can still be constructed, but the ring homomorphism from
can still be constructed, but the ring homomorphism from  to
to  might fail to be injective. For example, if
might fail to be injective. For example, if 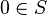 , then
, then  is the trivial ring.
is the trivial ring.
Notes
- ↑ Matsumura (1980), p. 12
- ↑ Matsumura (1989), p. 21
- ↑ Das, Abhijit; Madhavan, C. E. Veni (2009), Public-key Cryptography: Theory and Practice, Pearson Education India, p. 121, ISBN 9788131708323.
References
- Hideyuki Matsumura, Commutative algebra, 1980
- Hideyuki Matsumura, Commutative ring theory, 1989