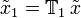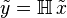Time-invariant system

From Wikipedia, the free encyclopedia

A time-invariant (TIV) system is one whose output does not depend explicitly on time.

If the input signal $x(t)$ produces an output $y(t)$ then any time shifted input, 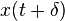$x(t+\delta )$ , results in a time-shifted output $y(t+\delta )$

This property can be satisfied if the transfer function of the system is not a function of time except expressed by the input and output. This property can also be stated in another way in terms of a schematic

If a system is time-invariant then the system block is commutative with an arbitrary delay.

Simple example

To demonstrate how to determine if a system is time-invariant then consider the two systems:

System A: $y(t)=t\,x(t)$
System B: $y(t)=10x(t)$

Since system A explicitly depends on t outside of $x(t)$ and $y(t)$ , it is not time-invariant. System B, however, does not depend explicitly on t so it is time-invariant.

Formal example

A more formal proof of why system A & B from above differ is now presented. To perform this proof, the second definition will be used.

System A:

Start with a delay of the input $x_{d}(t)=\,\!x(t+\delta )$

$y(t)=t\,x(t)$

$y_{1}(t)=t\,x_{d}(t)=t\,x(t+\delta )$

Now delay the output by $\delta$

$y(t)=t\,x(t)$

$y_{2}(t)=\,\!y(t+\delta )=(t+\delta )x(t+\delta )$

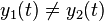Clearly $y_{1}(t)\,\!\neq y_{2}(t)$ , therefore the system is not time-invariant.

System B:

Start with a delay of the input $x_{d}(t)=\,\!x(t+\delta )$

$y(t)=10\,x(t)$

$y_{1}(t)=10\,x_{d}(t)=10\,x(t+\delta )$

Now delay the output by $\,\!\delta$

$y(t)=10\,x(t)$

$y_{2}(t)=y(t+\delta )=10\,x(t+\delta )$

Clearly $y_{1}(t)=\,\!y_{2}(t)$ , therefore the system is time-invariant. Although there are many other proofs, this is the easiest.

Abstract example

We can denote the shift operator by ${\mathbb {T}}_{r}$ where $r$ is the amount by which a vector's index set should be shifted. For example, the "advance-by-1" system

$x(t+1)=\,\!\delta (t+1)*x(t)$

can be represented in this abstract notation by

${\tilde {x}}_{1}={\mathbb {T}}_{1}\,{\tilde {x}}$

where ${\tilde {x}}$ is a function given by

${\tilde {x}}=x(t)\,\forall \,t\in {\mathbb {R}}$

with the system yielding the shifted output

${\tilde {x}}_{1}=x(t+1)\,\forall \,t\in {\mathbb {R}}$

So ${\mathbb {T}}_{1}$ is an operator that advances the input vector by 1.

Suppose we represent a system by an operator ${\mathbb {H}}$ . This system is time-invariant if it commutes with the shift operator, i.e.,

${\mathbb {T}}_{r}\,{\mathbb {H}}={\mathbb {H}}\,{\mathbb {T}}_{r}\,\,\forall \,r$

If our system equation is given by

${\tilde {y}}={\mathbb {H}}\,{\tilde {x}}$

then it is time-invariant if we can apply the system operator ${\mathbb {H}}$ on ${\tilde {x}}$ followed by the shift operator ${\mathbb {T}}_{r}$ , or we can apply the shift operator ${\mathbb {T}}_{r}$ followed by the system operator ${\mathbb {H}}$ , with the two computations yielding equivalent results.

Applying the system operator first gives

${\mathbb {T}}_{r}\,{\mathbb {H}}\,{\tilde {x}}={\mathbb {T}}_{r}\,{\tilde {y}}={\tilde {y}}_{r}$

Applying the shift operator first gives

${\mathbb {H}}\,{\mathbb {T}}_{r}\,{\tilde {x}}={\mathbb {H}}\,{\tilde {x}}_{r}$

If the system is time-invariant, then

${\mathbb {H}}\,{\tilde {x}}_{r}={\tilde {y}}_{r}$

Time-invariant system

Simple example

Formal example

Abstract example

See also