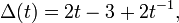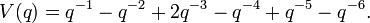Three-twist knot

From Wikipedia, the free encyclopedia

Three-twist knot

Arf invariant	0
Braid length	6
Braid no.	3
Bridge no.	2
Crosscap no.	2
Crossing no.	5
Hyperbolic volume	2.82812
Stick no.	8
Unknotting no.	1
Conway notation	[32]
A-B notation	5₂
Dowker notation	4, 8, 10, 2, 6
Last /Next	5₁ / 6₁
Other
alternating, hyperbolic, prime, reversible, twist

In knot theory, the three-twist knot is the twist knot with three-half twists. It is listed as the 5₂ knot in the Alexander-Briggs notation, and is one of two knots with crossing number five, the other being the cinquefoil knot.

The three-twist knot is a prime knot, and it is invertible but not amphichiral. Its Alexander polynomial is

$\Delta (t)=2t-3+2t^{{-1}},\,$

its Conway polynomial is

$\nabla (z)=2z^{2}+1,\,$

and its Jones polynomial is

$V(q)=q^{{-1}}-q^{{-2}}+2q^{{-3}}-q^{{-4}}+q^{{-5}}-q^{{-6}}.\,$ ^[1]

Because the Alexander polynomial is not monic, the three-twist knot is not fibered.

The three-twist knot is a hyperbolic knot, with its complement having a volume of approximately 2.82812.

References

↑ "5_2", The Knot Atlas.

v t e Knot theory (knots and links)

Hyperbolic	Figure-eight (4₁) Three-twist (5₂) Stevedore (6₁) 6₂ 6₃ Endless (7₄) Perko pair (10₁₆₁) (−2,3,7) pretzel (12n242) Borromean rings (63 2)

Satellite	Composite knots Granny Square

Torus	Unknot (0₁) Trefoil (3₁) Cinquefoil (5₁) Septafoil (7₁) Carrick mat (8₁₈) Unlink (02 1) Hopf (22 1) Solomon's (42 1) Whitehead (52 1) L10a140

Invariants	Alternating Arf invariant Bridge no. 2-bridge Brunnian Chirality Invertible Crosscap no. Crossing no. Finite type invariant Hyperbolic volume Genus Knot group Link group Linking no. Polynomial Alexander Bracket HOMFLY Jones Kauffman Pretzel Prime list Stick no. Tricolorability Unknotting no.

Notation & operations	Alexander–Briggs notation Conway notation Dowker notation Mutation Reidemeister move Skein relation

Other	Berge Braid theory Complement Double torus Fibered Framed Knot List of knots and links Ribbon Slice Sum Twist Wild

Category Commons

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.