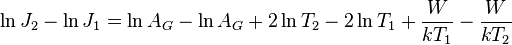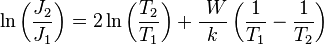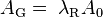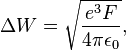Thermionic emission

From Wikipedia, the free encyclopedia
Closeup of the filament on a low pressure mercury gas discharge lamp showing white thermionic emission mix coating on the central portion of the coil. Typically made of a mixture of barium, strontium and calcium oxides, the coating is sputtered away through normal use, often eventually resulting in lamp failure.
One of the bulbs with which Edison discovered thermionic emission. It consists of an evacuated glass light bulb containing a carbon filament (hairpin shape), with an additional metal plate attached to wires emerging from the base. Electrons released by the filament were attracted to the plate when it had a positive voltage.

Thermionic emission is the heat-induced flow of charge carriers from a surface or over a potential-energy barrier. This occurs because the thermal energy given to the carrier overcomes the binding potential, also known as work function of the metal. The charge carriers can be electrons or ions, and in older literature are sometimes referred to as "thermions". After emission, a charge will initially be left behind in the emitting region that is equal in magnitude and opposite in sign to the total charge emitted. But if the emitter is connected to a battery, then this charge left behind will be neutralized by charge supplied by the battery, as the emitted charge carriers move away from the emitter, and finally the emitter will be in the same state as it was before emission. The thermionic emission of electrons is also known as thermal electron emission.

The classical example of thermionic emission is the emission of electrons from a hot cathode into a vacuum (also known as the Edison effect) in a vacuum tube. The hot cathode can be a metal filament, a coated metal filament, or a separate structure of metal or carbides or borides of transition metals. Vacuum emission from metals tends to become significant only for temperatures over 1000 K. The science dealing with this phenomenon has been known as thermionics, but this name seems to be gradually falling into disuse.

The term "thermionic emission" is now also used to refer to any thermally-excited charge emission process, even when the charge is emitted from one solid-state region into another. This process is crucially important in the operation of a variety of electronic devices and can be used for electricity generation (e.g., thermionic converters and electrodynamic tethers) or cooling. The magnitude of the charge flow increases dramatically with increasing temperature.

History

Because the electron was not identified as a separate physical particle until the 1897 work of J. J. Thomson, the word "electron" was not used when discussing experiments that took place before this date.

The phenomenon was initially reported in 1873 by Frederick Guthrie in Britain.[1] While doing work on charged objects, Guthrie discovered that a red-hot iron sphere with a negative charge would lose its charge (by somehow discharging it into air). He also found that this did not happen if the sphere had a positive charge.[2] Other early contributors included Johann Wilhelm Hittorf (1869–1883),[3] Eugen Goldstein (1885),[4] and Julius Elster and Hans Friedrich Geitel (1882–1889).[5]

The effect was rediscovered by Thomas Edison on February 13, 1880, while trying to discover the reason for breakage of lamp filaments and uneven blackening (darkest near one terminal of the filament) of the bulbs in his incandescent lamps.

Edison built several experiment bulbs, some with an extra wire, a metal plate, or foil inside the bulb which was electrically separate from the filament, and thus could serve as an electrode. He connected a galvanometer, a device used to measure current, to the output of the extra metal electrode. When the foil was charged negatively relative to the filament, no charge flowed between the filament and the foil. We now know that this was because the filament was emitting electrons, and thus were not attracted to the negatively charged foil. In addition, charge did not flow from the foil to the filament because the foil was not heated enough to emit charge (later called thermionic emission). However, when the foil was given a more positive charge than the filament, negative charge (in the form of electrons) could flow from the filament through the vacuum to the foil. This one-way current was called the Edison effect (although the term is occasionally used to refer to thermionic emission itself). He found that the current emitted by the hot filament increased rapidly with increasing voltage, and filed a patent application for a voltage-regulating device using the effect on November 15, 1883 (U.S. patent 307,031,[6] the first US patent for an electronic device). He found that sufficient current would pass through the device to operate a telegraph sounder. This was exhibited at the International Electrical Exposition in Philadelphia in September 1884. William Preece, a British scientist took back with him several of the Edison Effect bulbs, and presented a paper on them in 1885, where he referred to thermionic emission as the "Edison Effect."[7][8] The British physicist John Ambrose Fleming, working for the British "Wireless Telegraphy" Company, discovered that the Edison Effect could be used to detect radio waves. Fleming went on to develop the two-element vacuum tube known as the diode, which he patented on November 16, 1904.[9]

The thermionic diode can also be configured as a device that converts a heat difference to electric power directly without moving parts (a thermionic converter, a type of heat engine).

Following J. J. Thomson's identification of the electron, the British physicist Owen Willans Richardson began work on the topic that he later called "thermionic emission". He received a Nobel Prize in Physics in 1928 "for his work on the thermionic phenomenon and especially for the discovery of the law named after him".

Richardson's Law

In any solid metal, there are one or two electrons per atom that are free to move from atom to atom. This is sometimes collectively referred to as a "sea of electrons". Their velocities follow a statistical distribution, rather than being uniform, and occasionally an electron will have enough velocity to exit the metal without being pulled back in. The minimum amount of energy needed for an electron to leave a surface is called the work function. The work function is characteristic of the material and for most metals is on the order of several electronvolts. Thermionic currents can be increased by decreasing the work function. This often-desired goal can be achieved by applying various oxide coatings to the wire.

In 1901 Richardson published the results of his experiments: the current from a heated wire seemed to depend exponentially on the temperature of the wire with a mathematical form similar to the Arrhenius equation.[10] Later, he proposed that the emission law should have the mathematical form [11]

J=A_{{{\mathrm {G}}}}T^{2}{\mathrm {e}}^{{-W \over kT}}

where J is the emission current density, T is the temperature of the metal, W is the work function of the metal, k is the Boltzmann constant, and AG is a parameter discussed next.

Taking the logarithm of both sides

\ln J=\ln A_{G}+2\ln T-{{\frac {W}{{kT}}}}

Thus, the equation showing the relationship between current densities at two temperatures is

\ln J_{2}-\ln J_{1}=\ln A_{G}-\ln A_{G}+2\ln T_{2}-2\ln T_{1}+{{\frac {W}{{kT_{1}}}}-{\frac {W}{{kT_{2}}}}}
\ln \left({{\frac {{J_{2}}}{{J_{1}}}}}\right)=2\ln \left({{\frac {{T_{2}}}{{T_{1}}}}}\right)+{\frac {{\ W}}{k}}\left({{\frac {1}{{T_{1}}}}-{\frac {1}{{T_{2}}}}}\right)

In the period 1911 to 1930, as physical understanding of the behaviour of electrons in metals increased, various different theoretical expressions (based on different physical assumptions) were put forwards for AG, by Richardson, Saul Dushman, Ralph H. Fowler, Arnold Sommerfeld and Lothar Wolfgang Nordheim. Over 60 years later, there is still no consensus amongst interested theoreticians as to what the precise form of the expression for AG should be, but there is agreement that AG must be written in the form

A_{{{\mathrm {G}}}}=\;\lambda _{{{\mathrm {R}}}}A_{0}

where λR is a material-specific correction factor that is typically of order 0.5, and A0 is a universal constant given by [11]

A_{0}={4\pi mk^{2}e \over h^{3}}=1.20173\times 10^{6}\,{\mathrm {A\,m^{{-2}}\,K^{{-2}}}}

where m and −e are the mass and charge of an electron, and h is Planck's constant.

In fact, by about 1930 there was agreement that, due to the wave-like nature of electrons, some proportion rav of the outgoing electrons would be reflected as they reached the emitter surface, so the emission current density would be reduced, and λR would have the value (1-rav). Thus, one sometimes sees the thermionic emission equation written in the form

J=(1-r_{{{\mathrm {av}}}})A_{0}T^{2}{\mathrm {e}}^{{-W \over kT}}.

However, a modern theoretical treatment by Modinos assumes that the band-structure of the emitting material must also be taken into account. This would introduce a second correction factor λB into λR, giving 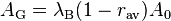A_{{{\mathrm {G}}}}=\lambda _{{{\mathrm {B}}}}(1-r_{{{\mathrm {av}}}})A_{0}. Experimental values for the "generalized" coefficient AG are generally of the order of magnitude of A0, but do differ significantly as between different emitting materials, and can differ as between different crystallographic faces of the same material. At least qualitatively, these experimental differences can be explained as due to differences in the value of λR.

Considerable confusion exists in the literature of this area because: (1) many sources do not distinguish between AG and A0, but just use the symbol A (and sometimes the name "Richardson constant") indiscriminately; (2) equations with and without the correction factor here denoted by λR are both given the same name; and (3) a variety of names exist for these equations, including "Richardson equation", "Dushman's equation", "Richardson–Dushman equation" and "Richardson–Laue–Dushman equation". In the literature, the elementary equation is sometimes given in circumstances where the generalized equation would be more appropriate, and this in itself can cause confusion. To avoid misunderstandings, the meaning of any "A-like" symbol should always be explicitly defined in terms of the more fundamental quantities involved.

Because of the exponential function, the current increases rapidly with temperature when kT is less than W. (For essentially every material, melting occurs well before kT = W.)

Schottky emission

Main article: Schottky effect

In electron emission devices, especially electron guns, the thermionic electron emitter will be biased negative relative to its surroundings. This creates an electric field of magnitude F at the emitter surface. Without the field, the surface barrier seen by an escaping Fermi-level electron has height W equal to the local work-function. The electric field lowers the surface barrier by an amount ΔW, and increases the emission current. This is known as the Schottky effect (named for Walter H. Schottky) or field enhanced thermionic emission. It can be modeled by a simple modification of the Richardson equation, by replacing W by (W − ΔW). This gives the equation[12][13]

J(F,T,W)=A_{{{\mathrm {G}}}}T^{2}e^{{-(W-\Delta W) \over kT}}
\Delta W={\sqrt {e^{3}F \over 4\pi \epsilon _{0}}},

where ε0 is the electric constant (also, formerly, called the vacuum permittivity).

Electron emission that takes place in the field-and-temperature-regime where this modified equation applies is often called Schottky emission. This equation is relatively accurate for electric field strengths lower than about 108 V  m−1. For electric field strengths higher than 108 V m−1, so-called Fowler-Nordheim (FN) tunneling begins to contribute significant emission current. In this regime, the combined effects of field-enhanced thermionic and field emission can be modeled by the Murphy-Good equation for thermo-field (T-F) emission.[14] At even higher fields, FN tunneling becomes the dominant electron emission mechanism, and the emitter operates in the so-called "cold field electron emission (CFE)" regime.

Thermionic emission can also be enhanced by interaction with other forms of excitation such as light.[15] For example, excited Cs-vapours in thermionic converters form clusters of Cs-Rydberg matter which yield a decrease of collector emitting work function from 1.5 eV to 1.0–0.7 eV. Due to long-lived nature of Rydberg matter this low work function remains low which essentially increases the low-temperature converter’s efficiency.[16]

Photon-enhanced thermionic emission

Photon-enhanced thermionic emission (PETE) is a process developed by engineers at Stanford University that harnesses both the light and heat of the sun to generate electricity and increases the efficiency of solar power production by more than twice the current levels. The device developed for the process reaches peak efficiency after it reaches 200°C; most silicon solar cells become inert after reaching 100°C. Such device will work best in parabolic trough collectors, which reach temperatures around 800°C. Although the team used a gallium nitride semiconductor in its "proof of concept" device, it claims that the use of gallium arsenide can increase the device's efficiency to 55–60 percent, nearly triple that of existing systems,[17][18] which is only 12–17 percent more than existing 43 percent multi-junction solar cells.[19]

See also

References

  1. ↑ See:
  2. ↑ Richardson, O. W. (2003). Thermionic Emission from Hot Bodies. Wexford College Press. p. 196. ISBN 978-1-929148-10-3. 
  3. ↑ See:
  4. ↑ E. Goldstein (1885) "Ueber electrische Leitung in Vacuum" (On electric conduction in vacuum) Annalen der Physik und Chemie, 3rd series, 24 : 79-92.
  5. ↑ See:
  6. ↑ Thomas A. Edison, "Electrical indicator," U.S. Patent 307,031 (filed: November 15, 1883 ; issued: October 21, 1884).
  7. ↑ William Henry Preece (1885) "On a peculiar behaviour of glow lamps when raised to high incandescence," Proceedings of the Royal Society of London, 38 : 219-230; on page 229, Preece coins the term the "Edison effect".
  8. ↑ Josephson, M. (1959). Edison. McGraw-Hill. ISBN 0-07-033046-8. 
  9. ↑ See:
    • Provisional specification for a thermionic valve was lodged on November 16, 1904. In this document, Fleming coined the British term "valve" for what in North America is called a "vacuum tube": "The means I employ for this purpose consists in the insertion in the circuit of the alternating current of an appliance which permits only the passage of electric current in one direction and constitutes therefore an electrical valve."
    • John Ambrose Fleming, "Improvements in instruments for detecting and measuring alternating electric currents," U.K. Patent 24,850 (filed: August 15, 1905 ; issued: September 21, 1905).
    • John Ambrose Fleming, "Instrument for converting alternating electric currents into continuous currents," U.S. Patent 803,684 (filed: April 29, 1905 ; issued: November 7, 1905). Download from: Google Patents.
  10. ↑ O. W. Richardson (1901) "On the negative radiation from hot platinum," Philosophical of the Cambridge Philosophical Society, 11 : 286-295.
  11. ↑ 11.0 11.1 Crowell, C. R. (1965). "The Richardson constant for thermionic emission in Schottky barrier diodes". Solid-State Electronics 8 (4): 395–399. Bibcode:1965SSEle...8..395C. doi:10.1016/0038-1101(65)90116-4. 
  12. ↑ Kiziroglou, M. E.; Li, X.; Zhukov, A. A.; De Groot, P. A. J.; De Groot, C. H. (2008). "Thermionic field emission at electrodeposited Ni-Si Schottky barriers". Solid-State Electronics 52 (7): 1032–1038. Bibcode:2008SSEle..52.1032K. doi:10.1016/j.sse.2008.03.002. 
  13. ↑ Orloff, J. (2008). "Schottky emission". Handbook of Charged Particle Optics (2nd ed.). CRC Press. pp. 5–6. ISBN 978-1-4200-4554-3. 
  14. ↑ Murphy, E. L.; Good, G. H. (1956). "Thermionic Emission, Field Emission, and the Transition Region". Physical Review 102 (6): 1464–1473. Bibcode:1956PhRv..102.1464M. doi:10.1103/PhysRev.102.1464. 
  15. ↑ Mal'Shukov, A. G.; Chao, K. A. (2001). "Opto-Thermionic Refrigeration in Semiconductor Heterostructures". Physical Review Letters 86 (24): 5570–5573. Bibcode:2001PhRvL..86.5570M. doi:10.1103/PhysRevLett.86.5570. 
  16. ↑ Svensson, R.; Holmlid, L. (1992). "Very low work function surfaces from condensed excited states: Rydber matter of cesium". Surface Science. 269/270: 695–699. Bibcode:1992SurSc.269..695S. doi:10.1016/0039-6028(92)91335-9. 
  17. ↑ Bergeron, L. (2 August 2010). "New solar energy conversion process discovered by Stanford engineers could revamp solar power production". Stanford Report. Retrieved 2010-08-04. 
  18. ↑ Schwede, J. W.; et al. (2010). "Photon-enhanced thermionic emission for solar concentrator systems". Nature Materials 9 (9): 762. Bibcode:2010NatMa...9..762S. doi:10.1038/nmat2814. 
  19. ↑ Green, M. A.; Emery, K.; Hishikawa, Y.; Warta, W. (2011). "Solar cell efficiency tables (version 37)". Progress in Photovoltaics: Research and Applications 19 (1): 84. doi:10.1002/pip.1088. 

External links

Theoretical principles
Types
Numbering systems
Examples
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.