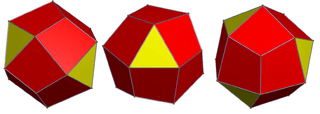
Tetrahedrally diminished dodecahedron
| Tetrahedrally diminished dodecahedron | |
|---|---|
 | |
| Conway polyhedron notation | pT |
| Faces | 16: 4 {3} + 12 {4} |
| Edges | 30 |
| Vertices | 16 |
| Vertex configuration | 3.4.4.4 4.4.4 |
| Symmetry group | T, [3,3]+, (233), order 12 |
| Dual polyhedron | Self-dual |
| Properties | convex |
In geometry, a tetrahedrally diminished dodecahedron or tetrahedrally truncated dodecahedron (also tetrahedrally stellated icosahedron) is a topologically self-dual polyhedron made of 16 vertices, 30 edges, and 16 faces (4 equilateral triangles and 12 identical quadrilaterals).[1] As a truncated regular dodecahedron, the quadrilaterals faces are trapezoids. Other geometric variation have the quadrilaterals as kites.
It has chiral tetrahedral symmetry, and so its geometry can be constructed from pyritohedral symmetry of the pseudoicosahedron with 4 faces stellated, or from the pyritohedron, with 4 vertices diminished (truncated with full edges removed). Within its tetrahedral symmetry, it has geometric varied proportions. By Dorman Luke dual construction, a unique geometric proportion can be defined. The kite faces have edges of length ratio ~ 1:0.6325.
As a self-dual hexadecahedron, it is one of 302404 forms, 1476 with at least order 2 symmetry, and the only one with tetrahedral symmetry.[2]
As a stellation of the icosahedron it is one of 32 stellations defined with tetrahedral symmetry.[3]
In Conway polyhedron notation, it can represented as pT, using George W. Hart's propeller operator.[4]
Related polytopes and honeycombs
This polyhedron represents the vertex figure of a hyperbolic uniform honeycomb, pt{3,5,3}, with 12 pentagonal antiprisms and 4 dodecahedron cells meeting at every vertex.

- Vertex figure projected as Schlegel diagram
References
External links
- tetrahedrally truncated dodecahedron and stellated icosahedron
- Generation of an icosahedron by the intersection of five tetrahedra: geometrical and crystallographic features of the intermediate polyhedra
- VRML model as truncated regular dodecahedron
- VRML model as tetrahedrally stellated icosahedron
| ||||||||||||||
| ||||||||||||||||||||||||||||