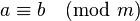Ternary relation

From Wikipedia, the free encyclopedia

In mathematics, a ternary relation or triadic relation is a finitary relation in which the number of places in the relation is three. Ternary relations may also be referred to as 3-adic, 3-ary, 3-dimensional, or 3-place.

Just as a binary relation is formally defined as a set of pairs, i.e. a subset of the Cartesian product A × B of some sets A and B, so a ternary relation is a set of triples, forming a subset of the Cartesian product A × B × C of three sets A, B and C.

An example of a ternary relation in elementary geometry is the collinearity of points.

Examples

Binary functions

Further information: Graph of a function and binary function

A function ƒ: A × B → C in two variables, taking values in two sets A and B, respectively, is formally a function that associates to every pair (a,b) in A × B an element ƒ(a, b) in C. Therefore its graph consists of pairs of the form ((a, b), ƒ(a, b)). Such pairs in which the first element is itself a pair are often identified with triples. This makes the graph of ƒ a ternary relation between A, B and C, consisting of all triples (a, b, ƒ(a, b)), for all a in A and b in B.

Cyclic orders

Main article: Cyclic order

Given any set A whose elements are arranged on a circle, one can define a ternary relation R on A, i.e. a subset of A3 = A × A × A, by stipulating that R(a, b, c) holds if and only if the elements a, b and c are pairwise different and when going from a to c in a clockwise direction one passes through b. For example if A = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 } represents the hours on a clock face, then R(8, 12, 4) holds and R(12, 8, 4) does not hold.

Betweenness relations

Congruence relation

The ordinary congruence of arithmetics

a\equiv b{\pmod {m}}

which holds for three integers a, b, and m if and only if m divides a - b, formally may be considered as a ternary relation. However, usually, this instead is considered as a family of binary relations between the a and the b, indexed by the modulus m. For each fixed m, indeed this binary relation has some natural properties, like being an equivalence relation; while the combined ternary relation in general is not studied as one relation.

Further reading

  • Myers, Dale (1997), "An interpretive isomorphism between binary and ternary relations", in Mycielski, Jan; Rozenberg, Grzegorz; Salomaa, Arto, Structures in Logic and Computer Science, Lecture Notes in Computer Science 1261, Springer, pp. 84–105, doi:10.1007/3-540-63246-8_6, ISBN 3-540-63246-8 
  • Novák, Vítězslav (1996), "Ternary structures and partial semigroups", Czechoslovak Mathematical Journal 46 (1): 111–120, hdl:10338.dmlcz/127275 
  • Novák, Vítězslav; Novotný, Miroslav (1989), "Transitive ternary relations and quasiorderings", Archivum Mathematicum 25 (1–2): 5–12, hdl:10338.dmlcz/107333 
  • Novák, Vítězslav; Novotný, Miroslav (1992), "Binary and ternary relations", Mathematica Bohemica 117 (3): 283–292, hdl:10338.dmlcz/126278 
  • Novotný, Miroslav (1991), "Ternary structures and groupoids", Czechoslovak Mathematical Journal 41 (1): 90–98, hdl:10338.dmlcz/102437 
  • Šlapal, Josef (1993), "Relations and topologies", Czechoslovak Mathematical Journal 43 (1): 141–150, hdl:10338.dmlcz/128381 

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.