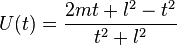Taub–NUT space

From Wikipedia, the free encyclopedia

General relativity
$G_{{\mu \nu }}+\Lambda g_{{\mu \nu }}={8\pi G \over c^{4}}T_{{\mu \nu }}$
Introduction Mathematical formulation Resources · Tests
Fundamental concepts Special relativity Equivalence principle World line · Riemannian geometry
Phenomena Kepler problem · Lenses · Waves Frame-dragging · Geodetic effect Event horizon · Singularity Black hole
Equations Linearized gravity Post-Newtonian formalism Einstein field equations Geodesic equation Mathisson–Papapetrou–Dixon equations‎ Friedmann equations ADM formalism BSSN formalism Hamilton–Jacobi–Einstein equation
Advanced theories Kaluza–Klein Quantum gravity
Solutions Schwarzschild Reissner–Nordström · Gödel Kerr · Kerr–Newman Kasner · Taub-NUT · Milne · Robertson–Walker pp-wave · van Stockum dust
Scientists Einstein · Lorentz · Hilbert · Poincaré · Schwarzschild · Sitter · Reissner · Nordström · Weyl · Eddington · Friedman · Milne · Zwicky · Lemaître · Gödel · Wheeler · Robertson · Bardeen · Walker · Kerr · Chandrasekhar · Ehlers · Penrose · Hawking · Taylor · Hulse · Stockum · Taub · Newman · Yau · Thorne others
Spacetime Spacetime Minkowski spacetime Spacetime diagrams Spacetime in General relativity
v t e

The Taub–NUT space (/tɑːb nʌt/^[1] or /tɑːb ɛnjuːˈtiː/) is an exact solution to Einstein's equations, a model universe formulated in the framework of general relativity.

The Taub–NUT metric was found by Abraham Haskel Taub (1951), and extended to a larger manifold by E. Newman, L. Tamburino, and T. Unti (1963), whose initials form the "NUT" of "Taub–NUT".

Taub's solution is an empty space solution of Einstein's equations with topology R×S³ and metric

$ds^{2}=-dt^{2}/U(t)+4l^{2}U(t)(d\psi +\cos \theta d\phi )^{2}+(t^{2}+l^{2})(d\theta ^{2}+(\sin \theta )^{2}d\phi ^{2})$

where

$U(t)={\frac {2mt+l^{2}-t^{2}}{t^{2}+l^{2}}}$

and m and l are positive constants.

Taub's metric has coordinate singularities at U=0, t=m+(m²+l²)^1/2, and Newman, Tamburino and Unti showed how to extend the metric across these surfaces.

References

↑ McGraw-Hill Science & Technology Dictionary: "Taub NUT space"

Newman, E.; Tamburino, L.; Unti, T. (1963), "Empty-space generalization of the Schwarzschild metric", Journal of Mathematical Physics 4: 915–923, Bibcode:1963JMP.....4..915N, doi:10.1063/1.1704018, ISSN 0022-2488, MR 0152345
Taub, A. H. (1951), "Empty space-times admitting a three parameter group of motions", Annals of Mathematics. Second Series 53: 472–490, ISSN 0003-486X, MR 0041565 JSTOR 1969567

Relativity

Special
relativity

Background	Principle of relativity Introduction to special relativity Special relativity

Foundations	Relative motion Frame of reference Speed of light Maxwell's equations

Formulation	Galilean relativity Galilean transformation Lorentz transformation

Consequences	Time dilation Relativistic mass Mass–energy equivalence Length contraction Relativity of simultaneity Relativistic Doppler effect Thomas precession Relativistic disks

Spacetime	Minkowski spacetime World line Spacetime diagrams Light cone

General
relativity

Background	Introduction Mathematical formulation Resources

Fundamental concepts	Special relativity Equivalence principle World line Riemannian geometry Spacetime diagrams Spacetime in General relativity

Phenomena	Kepler problem Lenses Waves Frame-dragging Geodetic effect Event horizon Singularity Black hole

Equations	Linearized gravity Post-Newtonian formalism Einstein field equations Geodesic equation Friedmann equations ADM formalism BSSN formalism Hamilton–Jacobi–Einstein equation

Advanced theories	Kaluza–Klein Quantum gravity

Solutions	Schwarzschild Reissner–Nordström Gödel Kerr Kerr–Newman Kasner Taub-NUT Milne Robertson–Walker pp-wave van Stockum dust

Scientists

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.