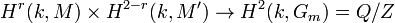Tate duality
From Wikipedia, the free encyclopedia
In mathematics, Tate duality or Poitou–Tate duality is a duality theorem for Galois cohomology groups of modules over the Galois group of an algebraic number field or local field, introduced by Tate (1962) and Poitou (1967).
Local Tate duality
Main article: local Tate duality
Local Tate duality says there is a perfect pairing of finite groups
where M is a finite group scheme and M′ its dual Hom(M,Gm).
See also
References
- Haberland, Klaus (1978), Galois cohomology of algebraic number fields, VEB Deutscher Verlag der Wissenschaften, MR 519872
- Poitou, Georges (1967), "Propriétés globales des modules finis", Cohomologie galoisienne des modules finis, Séminaire de l'Institut de Mathématiques de Lille, sous la direction de G. Poitou. Travaux et Recherches Mathématiques, 13, Paris: Dunod, pp. 255–277, MR 0219591
- Tate, John (1963), "Duality theorems in Galois cohomology over number fields", Proceedings of the International Congress of Mathematicians (Stockholm, 1962), Djursholm: Inst. Mittag-Leffler, pp. 288–295, MR 0175892
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.