Tangential angle
.png)
 for an arbitrary curve P
for an arbitrary curve PIn geometry, the tangential angle of a curve in the Cartesian plane, at a specific point, is the angle between the tangent line to the curve at the given point and the x-axis.[1] (Note, some authors define the angle as the deviation from the direction of the curve at some fixed starting point. This is equivalent to the definition given here by the addition of a constant to the angle or by rotating the curve.[2])
Equations
If a curve is given parametrically by  , then the tangential angle
, then the tangential angle  at
at 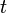 is defined (up to a multiple of
is defined (up to a multiple of  ) by[3]
) by[3]
Here, the prime symbol denotes derivative. Thus, the tangential angle specifies the direction of the velocity vector  , while the speed specifies its magnitude. The vector
, while the speed specifies its magnitude. The vector  is called the unit tangent vector, so an equivalent definition is that the tangential angle at
is called the unit tangent vector, so an equivalent definition is that the tangential angle at 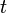 is the angle
is the angle  such that
such that 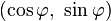 is the unit tangent vector at
is the unit tangent vector at 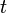 .
.
If the curve is parameterized by arc length  , so
, so  , then the definition simplifies to
, then the definition simplifies to  . In this case, the curvature
. In this case, the curvature  is given by
is given by 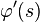 , where
, where  is taken to be positive if the curve bends to the left and negative if the curve bends to the right.[4]
is taken to be positive if the curve bends to the left and negative if the curve bends to the right.[4]
If the curve is given by  , then we may take
, then we may take 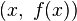 as the parameterization, and we may assume
as the parameterization, and we may assume  is between
is between 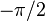 and
and  . This produces the explicit expression
. This produces the explicit expression  .
.
Polar tangential angle
In polar coordinates, define the polar tangential angle as the angle between the tangent line to the curve at the given point and ray from the origin to the point.[5] If  denotes the polar tangential angle, then
denotes the polar tangential angle, then 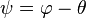 , where
, where  is as above and
is as above and 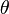 is, as usual, the polar angle.
is, as usual, the polar angle.
If the curve is defined in polar coordinates by 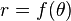 , then polar tangential angle
, then polar tangential angle  at
at 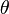 is defined (up to a multiple of
is defined (up to a multiple of  ) by
) by
-
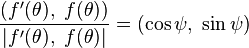 .
.
If the curve is parameterized by arc length  as
as  , so
, so  , then the definition becomes
, then the definition becomes  .
.
The logarithmic spiral can be defined a curve whose polar tangential angle is constant.[5][6]
See also
References
- ↑ "Natural Equation" at MathWorld
- ↑ For example W. Whewell "Of the Intrinsic Equation of a Curve, and its Application" Cambridge Philosophical Transactions Vol. VIII (1849) pp. 659-671. Google Books uses φ to mean the angle between the tangent and tangent at the origin. This is the paper introducing the Whewell equation, an application of the tangential angle.
- ↑ MathWorld "Tangential Angle"
- ↑ MathWorld "Natural Equation" differentiating equation 1
- ↑ 5.0 5.1 "Logarithmic Spiral" at Planet Math
- ↑ Williamson for section unless otherwise noted.
- Weisstein, Eric W., "Tangential Angle", MathWorld.
- Weisstein, Eric W., "Natural Equation", MathWorld.
- "Notations" at Encyclopédie des Formes Mathématiques Remarquables
- R.C. Yates (1952). A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards. pp. 123–126.
- "Angle between Tangent and Radius Vector" in An elementary treatise on the differential calculus By Benjamin Williamson p222 9th ed. (1899) online
