Tangent indicatrix

From Wikipedia, the free encyclopedia

In differential geometry, the tangent indicatrix of a closed space curve is a curve on the unit sphere intimately related to the curvature of the original curve. Let 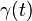$\gamma (t)\,$ be a closed curve with nowhere-vanishing tangent vector 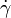${\dot {\gamma }}$ . Then the tangent indicatrix $T(t)\,$ of $\gamma \,$ is the closed curve on the unit sphere given by 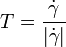$T={\frac {{\dot {\gamma }}}{|{\dot {\gamma }}|}}$ .

The total curvature of $\gamma \,$ (the integral of curvature with respect to arc length along the curve) is equal to the arc length of $T\,$ .

References

Solomon, B. "Tantrices of Spherical Curves." Amer. Math. Monthly 103, 30-39, 1996.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.