T-square (fractal)

From Wikipedia, the free encyclopedia
This article is about a two dimensional fractal in mathematics. For other uses, see T-square (disambiguation).

In mathematics, the T-square is a two-dimensional fractal. As all two-dimensional fractals, it has a boundary of infinite length bounding a finite area. Its name follows from that for a T-square.


Algorithmic description

It can be generated from using this algorithm:

  1. Image 1:
    1. Start with a square.
    2. Subtract a square half the original length and width (one-quarter the area) from the center.
  2. Image 2:
    1. Start with the previous image.
    2. Scale down a copy to one-half the original length and width.
    3. From each of the quadrants of Image 1, subtract the copy of the image.
  3. Images 3–6:
    1. Repeat step 2.
T-square.

The method of creation is rather similar to the ones used to create a Koch snowflake or a Sierpinski triangle.

Properties

T-square has a fractal dimension of ln(4)/ln(2) = 2.[citation needed] The black surface extent is almost everywhere in the bigger square, for, once a point has been darkened, it remains black for every other iteration ; however some points remain white.

The fractal dimension of the boundary equals 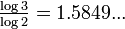\textstyle {{\frac {\log {3}}{\log {2}}}=1.5849...}.

See also

References

  • Hamma, Alioscia; Lidar, Daniel A.; Severini, Simone (2010). "Entanglement and area law with a fractal boundary in topologically ordered phase". Phys. Rev. A 82. doi:10.1103/PhysRevA.81.010102. 
  • Ahmed, Emad S. (2012). "Dual-mode dual-band microstrip bandpass filter based on fourth iteration T-square fractal and shorting pin". Radioengineering 21 (2): 617. 
Characteristics
Iterated function system
Strange attractor
L-system
Escape-time fractals
Random fractals
People
Other
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.