T-J model

From Wikipedia, the free encyclopedia

The t-J model was first derived in 1977 from the Hubbard model by Józef Spałek. The model describes strongly correlated electron systems. It is used to calculate high temperature superconductivity states in doped antiferromagnets.

The t-J Hamiltonian is:

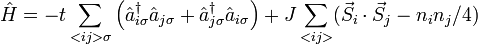
${\hat H}=-t\sum _{{<ij>\sigma }}\left({\hat a}_{{i\sigma }}^{\dagger }{\hat a}_{{j\sigma }}+{\hat a}_{{j\sigma }}^{\dagger }{\hat a}_{{i\sigma }}\right)+J\sum _{{<ij>}}({\vec S}_{{i}}\cdot {\vec S}_{{j}}-n_{i}n_{j}/4)$

where

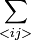$\sum _{{<ij>}}$ - sum over nearest-neighbor sites i and j,

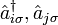${\hat a}_{{i\sigma }}^{\dagger },{\hat a}_{{j\sigma }}$ - fermionic creation and annihilation operators,

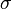$\sigma$ - spin polarization,

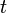$t$ - hopping integral

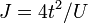$J$ - coupling constant $J=4t^{2}/U$ ,

$U$ - coulomb repulsion,

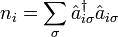$n_{{i}}=\sum _{{\sigma }}{\hat a}_{{i\sigma }}^{\dagger }{\hat a}_{{i\sigma }}$ - particle number at the site i, and

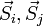${\vec S}_{i},{\vec S}_{j}$ - spins on the sites i and j.

References

t-J model then and now: A personal perspective from the pioneering times, Józef Spałek, arXiv:0706.4236

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.