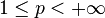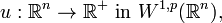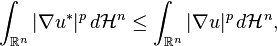Szegő inequality

From Wikipedia, the free encyclopedia

In functional analysis, a mathematical discipline, the Szegő inequality or Pólya–Szegő inequality, named after George Pólya and Gábor Szegő, states that if

1\leq p<+\infty

and

u:{\mathbb {R}}^{n}\rightarrow {\mathbb {R}}^{+}{\text{ in }}W^{{1,p}}({\mathbb {R}}^{n}),

then

\int _{{{\mathbb {R}}^{n}}}|\nabla u^{*}|^{p}\,d{\mathcal {H}}^{n}\leq \int _{{{\mathbb {R}}^{n}}}|\nabla u|^{p}\,d{\mathcal {H}}^{n},

where u^{*} is the symmetric decreasing rearrangement of u.

See also


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.