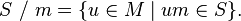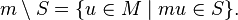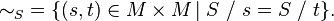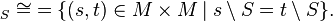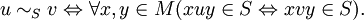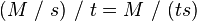Syntactic monoid

From Wikipedia, the free encyclopedia

In mathematics and computer science, the syntactic monoid M(L) of a formal language L is the smallest monoid that recognizes the language L.

Syntactic quotient

Given 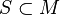$S\subset M$ of a monoid M of every string over some alphabet, one may define sets that consist of formal left or right inverses of elements in S. These are called quotients, and one may define right or left quotients, depending on which side one is concatenating. Thus, the right quotient of S by an element $m\in M$ is the set

$S\ /\ m=\{u\in M\;\vert \;um\in S\}.$

Similarly, the left quotient is

$m\setminus S=\{u\in M\;\vert \;mu\in S\}.$

Syntactic equivalence

The syntactic quotient induces an equivalence relation on M, called the syntactic relation, or syntactic equivalence (induced by S). The right syntactic equivalence is the equivalence relation

$\sim _{S}\;=\{(s,t)\in M\times M\,\vert \;S\ /\ s=S\ /\ t\}.$

Similarly, the left syntactic relation is

$\,_{S}\cong \;=\{(s,t)\in M\times M\,\vert \;s\setminus S=t\setminus S\}.$

The syntactic congruence may be defined as^[1]

$u\sim _{S}v\Leftrightarrow \forall x,y\in M(xuy\in S\Leftrightarrow xvy\in S).$

The definition extends to a congruence defined by a subset S of a general monoid M. A disjunctive set is a subset S such that the syntactic congruence defined by S is the equality relation.^[2]

Syntactic monoid

The syntactic quotient is compatible with concatenation in the monoid, in that one has

$(M\ /\ s)\ /\ t=M\ /\ (ts)$

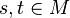for all $s,t\in M$ (and similarly for the left quotient). Thus, the syntactic quotient is a monoid morphism, and induces a quotient monoid

$M(S)=M\ /\ \sim _{S}.$

This monoid 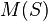$M(S)$ is called the syntactic monoid of S. It can be shown that it is the smallest monoid that recognizes S ; that is, M(S) recognizes S, and for every monoid N recognizing S, M(S) is a quotient of a submonoid of N. The syntactic monoid of S is also the transition monoid of the minimal automaton of S.^[1]^[3]

Similarly, a language L is regular if and only if the family of quotients

$\{m\setminus L\,\vert \;m\in M\}$

is finite. The proof showing equivalence is quite easy. Assume that a string x is read by a deterministic finite automaton, with the machine proceeding into state p. If y is another string read by the machine, also terminating in the same state p, then clearly one has 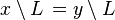$x\setminus L\,=y\setminus L$ . 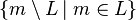Thus, the number of elements in $\{m\setminus L\,\vert \;m\in M\}$ is just exactly equal to the number of states of the automaton and $\{m\setminus L\,\vert \;m\in L\}$ is equal to number of final states. Assume the converse: that the number of elements in $\{m\setminus L\,\vert \;m\in M\}$ is finite. 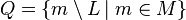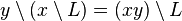One can then construct an automaton where $Q=\{m\setminus L\,\vert \;m\in M\}$ is the set of states, $F=\{m\setminus L\,\vert \;m\in L\}$ is the set of final states, the language L is the initial state, and the transition function is given by $y\setminus (x\setminus L)=(xy)\setminus L$ . Clearly, this automaton recognizes L. Thus, a language L is recognizable if and only if the set $\{m\setminus L\,\vert \;m\in M\}$ is finite.

Given a regular expression E representing S, it is easy to compute the syntactic monoid of S.

A group language is one for which the syntactic monoid is a group.^[4]

Examples

Let L be the language over A = {a,b} of words of even length. The syntactic congruence has two classes, L itself and L₁, the words of odd length. The syntactic monoid is the group of order 2 on {L,L₁}.^[5]
The bicyclic monoid is the syntactic monoid of the Dyck language (the language of balanced sets of parentheses).
The free monoid on A is the syntactic monoid of the language { ww^R | w in A* }, where w^R denotes the reversal of word w.
Every finite monoid is homomorphic to the syntactic monoid of some non-trivial language,^[6] but not every finite monoid is isomorphic to a syntactic monoid.^[7]
Every finite group is isomorphic to the syntactic monoid of some non-trivial language.^[6]
The language over {a,b} in which the number of occurrences of a and b are congruent modulo 2ⁿ is a group language with syntactic monoid Z/2ⁿ.^[4]
Trace monoids are examples of syntactic monoids.
Marcel-Paul Schützenberger^[8] characterized star-free languages as those with finite aperiodic syntactic monoids.^[9]

References

↑ 1.0 1.1 Lawson (2004) p.210
↑ Lawson (2004) p.232
↑ Straubing (1994) p.55
↑ 4.0 4.1 Sakarovitch (2009) p.342
↑ Straubing (1994) p.54
↑ 6.0 6.1 McNaughton, Robert; Papert, Seymour (1971). Counter-free Automata. Research Monograph 65. With an appendix by William Henneman. MIT Press. p. 48. ISBN 0-262-13076-9. Zbl 0232.94024.
↑ Lawson (2004) p.233
↑ Marcel-Paul Schützenberger (1965). "On finite monoids having only trivial subgroups". Information and Computation 8 (2): 190–194.
↑ Straubing (1994) p.60

Anderson, James A. (2006). Automata theory with modern applications. With contributions by Tom Head. Cambridge: Cambridge University Press. ISBN 0-521-61324-8. Zbl 1127.68049.
Lawson, Mark V. (2004). Finite automata. Chapman and Hall/CRC. ISBN 1-58488-255-7. Zbl 1086.68074.
Pin, Jean-Eric (1997). "10. Syntactic semigroups". In Rozenberg, G.; Salomaa, A. Handbook of Formal Language Theory 1. Springer-Verlag. pp. 679–746. Zbl 0866.68057.
Sakarovitch, Jacques (2009). Elements of automata theory. Translated from the French by Reuben Thomas. Cambridge University Press. ISBN 978-0-521-84425-3. Zbl 1188.68177.
Straubing, Howard (1994). Finite automata, formal logic, and circuit complexity. Progress in Theoretical Computer Science. Basel: Birkhäuser. ISBN 3-7643-3719-2. Zbl 0816.68086.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.