SymPy

From Wikipedia, the free encyclopedia
Not to be confused with SimPy, a discrete-event simulation language.
SymPy
Developer(s) Independent group of people
Initial release 2007 (2007)
Stable release 0.7.4.1 / December 15, 2013 (2013-12-15)
Development status Active
Written in Python
Operating system Cross-platform
Type Computer algebra system
License New BSD license
Website sympy.org

SymPy is a Python library for symbolic computation. The stated goals of the library are to become a full-featured computer algebra system and to keep a simple code base to promote extensibility and comprehensibility. SymPy is written entirely in Python and does not depend on any additional libraries.[1] It is available both as a desktop application and on the web as SymPy Live.

SymPy includes features ranging from basic symbolic arithmetic to calculus, algebra, discrete mathematics and quantum physics. It is capable of formatting the result of the computations as LaTeX code.[1]

SymPy is free software and is licensed under New BSD license. The lead developers are Ondřej Čertík and Aaron Meurer.

Features

The SymPy library is split into a core with many optional modules.

Currently, the core of SymPy has around 13,000 lines of code (including comments and docstrings) and its capabilities include:[1]

Core capabilities

  • Basic arithmetic: *, /, +, -, **
  • Simplification
  • Expansion
  • Functions: trigonometric, hyperbolic, exponential, roots, logarithms, absolute value, spherical harmonics, factorials and gamma functions, zeta functions, polynomials, hypergeometric, special functions, ...
  • Substitution
  • Arbitrary precision integers, rationals and floats
  • Noncommutative symbols
  • Pattern matching

Polynomials

Calculus

Solving Equations

Discrete math

  • Binomial coefficients
  • Summations
  • Products
  • Number theory: generating prime numbers, primality testing, integer factorization, ...
  • Logic expressions

Matrices

  • Basic arithmetic
  • Eigenvalues/eigenvectors
  • Determinants
  • Inversion
  • Solving

Geometry

  • Points, lines, rays, segments, ellipses, circles, polygons, ...
  • Intersections
  • Tangency
  • Similarity

Plotting

Note, plotting requires the external Pyglet module.

  • Coordinate models
  • Plotting Geometric Entities
  • 2D and 3D
  • Interactive interface
  • Colors

Physics

Statistics

Printing

  • Pretty printing: ASCII/Unicode pretty printing, LaTeX
  • Code generation: C, FORTRAN, Python

Summary

The complete set of SymPy modules are over 300,000 lines including documentation and tests as of version 0.7.1.

SymPy also includes a comprehensive set of self-tests (over 56,000 lines in 210 files as of version 0.7.1).

Related projects

  • Sage: an open source alternative to Mathematica, Maple, Matlab, and Magma (SymPy is included in Sage)
  • mpmath: a Python library for arbitrary-precision floating-point arithmetic (included in SymPy)
  • sympycore: another Python computer algebra system
  • symbide: GUI for SymPy in PyGTK
  • symfe: Lightweight symbolic finite element calculations in Python

Optional dependencies

SymPy requires no dependencies other than Python to run, but there are several optional dependencies that can enhance its capabilities:

  • Pyglet: This module is required for plotting
  • gmpy: If gmpy is installed, the SymPy's polynomial module will automatically use it for faster ground types. This can provide a several times boost in performance of certain operations.

Usage examples

Pretty Printing

Sympy allows outputs to be formatted into a more appealing format through the pprint function. Alternatively, the init_printing() method will enable pretty printing, so pprint need not be called. Pretty printing will use unicode symbols when available in the current environment, otherwise it will fall back to ASCII characters.

>>> from sympy import pprint, init_printing, Symbol, sin, cos, exp, sqrt, series, Integral, Function
>>>
>>> x = Symbol("x")
>>> y = Symbol("y")
>>> f = Function('f')
>>> # pprint will default to unicode if available
>>> pprint( x**exp(x) )
 ⎛ x⎞
 ⎝ℯ ⎠
x   
>>> # An output without unicode
>>> pprint(Integral(f(x), x), use_unicode=False)
  /       
 |        
 | f(x) dx
 |        
/        
>>> # Compare with same expression but this time unicode is enabled
>>> pprint(Integral(f(x), x), use_unicode=True)
⌠        
⎮ f(x) dx
⌡     
>>> # Alternatively, you can call init_printing() once and pretty print without the pprint function.
>>> init_printing()
>>> sqrt(sqrt(exp(x)))
 x
 ─
 4
ℯ 
>>> (1/cos(x)).series(x, 0, 10)
     2      4       6        8         
    x    5⋅x    61⋅x    277⋅x     ⎛ 10⎞
1 + ── + ──── + ───── + ────── + O⎝x  ⎠
    2     24     720     8064

Expansion

>>> from sympy import init_printing, Symbol, expand
>>> init_printing()
>>>
>>> a = Symbol('a')
>>> b = Symbol('b')
>>> e = (a + b)**5
>>> e
       5
(a + b) 
>>> e.expand()
 5      4        3  2       2  3       4    5
a  + 5⋅a ⋅b + 10⋅a ⋅b  + 10⋅a ⋅b  + 5⋅a⋅b  + b

Arbitrary Precision Example

>>> from sympy import Rational, pprint
>>>
>>> e = Rational(2)**50 / Rational(10)**50
>>> pprint(e)
1/88817841970012523233890533447265625

Differentiation

>>> from sympy import init_printing, symbols, ln, diff
>>> init_printing()
>>> x,y = symbols('x y')
>>> f = x**2 / y + 2 * x - ln(y)
>>> diff(f,x)
 2⋅x    
 ─── + 2
  y 
>>> diff(f,y)
    2    
   x    1
 - ── - ─
    2   y
   y
>>> diff(diff(f,x),y)
 -2⋅x
 ────
   2 
  y

Plotting

Output of the plotting example
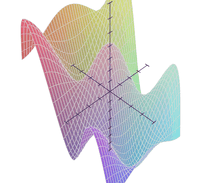
>>> from sympy import symbols, Plot, cos
>>> x,y = symbols('x y')
>>> Plot(cos(x*3)*cos(y*5)-y)
[0]: -y + cos(3*x)*cos(5*y), 'mode=cartesian'

Limits

>>> from sympy import init_printing, Symbol, limit, sqrt, oo
>>> init_printing()
>>> 
>>> x = Symbol('x')
>>> limit(sqrt(x**2 - 5*x + 6) - x, x, oo)
-5/2
>>> limit(x*(sqrt(x**2 + 1) - x), x, oo)
1/2
>>> limit(1/x**2, x, 0)
∞
>>> limit(((x - 1)/(x + 1))**x, x, oo)
 -2
ℯ

Differential Equations

>>> from sympy import init_printing, Symbol, Function, Eq, dsolve, sin, diff
>>> init_printing()
>>>
>>> x = Symbol("x")
>>> f = Function("f")
>>>
>>> eq = Eq(f(x).diff(x), f(x))
>>> eq
d              
──(f(x)) = f(x)
dx         
>>>    
>>> dsolve(eq, f(x))
           x
f(x) = C₁⋅ℯ
 
>>>
>>> eq = Eq(x**2*f(x).diff(x), -3*x*f(x) + sin(x)/x)
>>> eq
 2 d                      sin(x)
x ⋅──(f(x)) = -3⋅x⋅f(x) + ──────
   dx                       x   
>>>
>>> dsolve(eq, f(x))
       C₁ - cos(x)
f(x) = ───────────
             3    
            x

Integration

>>> from sympy import init_printing, integrate, Symbol, exp, cos, erf
>>> init_printing()
>>> x = Symbol('x')
>>> # Polynomial Function
>>> f = x**2 + x + 1
>>> f
 2        
x  + x + 1
>>> integrate(f,x)
 3    2    
x    x     
── + ── + x
3    2     
>>> # Rational Function
>>> f = x/(x**2+2*x+1)
>>> f
     x      
────────────
 2          
x  + 2⋅x + 1
 
>>> integrate(f, x)
               1  
log(x + 1) + ─────
             x + 1
>>> # Exponential-polynomial functions
>>> f = x**2 * exp(x) * cos(x)
>>> f
 2  x       
x ⋅ℯ ⋅cos(x)
>>> integrate(f, x)
 2  x           2  x                         x           x       
x ⋅ℯ ⋅sin(x)   x ⋅ℯ ⋅cos(x)      x          ℯ ⋅sin(x)   ℯ ⋅cos(x)
──────────── + ──────────── - x⋅ℯ ⋅sin(x) + ───────── - ─────────
     2              2                           2           2    
>>> # A non-elementary integral
>>> f = exp(-x**2) * erf(x)
>>> f
   2       
 -x        
ℯ   ⋅erf(x)
>>> integrate(f, x)
 
  ___    2   
╲╱ π ⋅erf (x)
─────────────
      4

Series

>>> from sympy import Symbol, cos, sin, pprint
>>> x = Symbol('x')
>>> e = 1/cos(x)
>>> pprint(e)
  1   
──────
cos(x)
>>> pprint(e.series(x, 0, 10))
     2      4       6        8         
    x    5⋅x    61⋅x    277⋅x     ⎛ 10⎞
1 + ── + ──── + ───── + ────── + O⎝x  ⎠
    2     24     720     8064          
>>> e = 1/sin(x)
>>> pprint(e)
  1   
──────
sin(x)
>>> pprint(e.series(x, 0, 4))
           3        
1   x   7⋅x     ⎛ 4⎞
─ + ─ + ──── + O⎝x ⎠
x   6   360

See also

  • Comparison of computer algebra systems

References

  1. ↑ 1.0 1.1 1.2 "SymPy homepage". Retrieved 2013-09-17. 

External links

Retail
Open source
Free/shareware
Discontinued
  • Category
  • Comparison
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.