Surprise (networks)

From Wikipedia, the free encyclopedia

Surprise (denoted S) is a global measure of the quality of a partition of a given complex network into communities. The name Surprise derives from the fact that its value evaluates how surprising (unlikely) is, from a statistical point of view, a given partition. Using benchmarks with networks with known community structure, it has been shown that Surprise maximization is a very effective way to determine the communities present in the networks.

Definition

Formula

Given a partition into communities, Surprise compares the number of links within and between communities in that partition with the expected number of them in a random network with the same distribution of nodes per communities. Thus, S evaluates, at the same time, both the number of nodes and links.

The formula of Surprise for a given partition is:[1]

S=-\log \sum _{{j=p}}^{{\min(M,n)}}{\frac {{\binom {M}{j}}{\binom {F-M}{n-j}}}{{\binom {F}{n}}}}

where F is the maximum possible number of links in the network for the number of nodes k

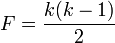
F={\frac {k(k-1)}{2}}

M is the maximum possible number of intra-community links. Let C be the number of communities, then

M=\sum _{{i=1}}^{{C}}{\frac {k_{i}(k_{i}-1)}{2}}

n is the actual number of links in the network and p is the actual number of intra-community links of that partition.

Properties

  • S values range between zero and plus infinity
  • S becomes zero in the following two cases:
  • All nodes are joined into a single community
  • Each node has its own community

Surprise-based algorithms

The fact that Surprise allows for a precise characterization of the quality of a partition suggests that it can be also used as a criterion to develop high-quality algorithms for community detection.

There are currently three algorithms, UVCLUSTER, SCLUSTER and RCLUSTER, which use Surprise maximization to determine the best partition in a hierarchical tree generated from a graph using consensus clustering.[2] The oldest algorithm, UVCLUSTER [3] is the best known, having been used or discussed in over 150 papers.[4] However, no Surprise maximizer algorithm has been devised so far. It has been shown that maximizing S is an NP-hard problem.[5]

Recently, SurpriseMe, an integrated tool that establishes which among seven state-of-the-art algorithms generates the maximum Surprise value, has been described. [6] SurpriseMe allows also to easily compare the results of the seven algorithms, by generating trees based on distances that correspond to how different are the partitions generated by each algorithm.

A new paradigm in community detection

The analysis of community structure in networks is of great importance in many scientific fields and, therefore, how to optimally detect these communities has been object of research in recent years. In 2004, Newman and Girvan proposed modularity (Q)[7] as a benefit function to evaluate the quality of the partition into communities of a network. Although Q has been widely used, it is known to have serious problems. For example, it has been demonstrated that Q suffers a resolution limit.[8] That is, the measure is unable to detect communities smaller than a certain threshold, which is determined by the size of the network. Although several attempts to avoid this limitation have been proposed, none of them solves it in a general manner.

Rodrigo and Marín argue S has theoretical advantages over Q and Q-based indexes. While these measures evaluate the quality of the partition based on the density of links, regardless of the number of nodes; S takes into account both the number of nodes and links. Moreover, Q computes the quality of the partition by summing the individual qualities of the different communities. On the contrary, S evaluates the quality of the whole partition at the same time.

See also

References

  1. ↑ Rodrigo Aldecoa and Ignacio Marín (2011). "Deciphering network community structure by Surprise". PLoS ONE 6 (9): e24195. doi:10.1371/journal.pone.0024195. PMID 21909420. 
  2. ↑ Rodrigo Aldecoa and Ignacio Marín (2010). "Jerarca: Efficient Analysis of Complex Networks Using Hierarchical Clustering". PLoS ONE 5: e11585. doi:10.1371/journal.pone.0011585. 
  3. ↑ Vicente Arnau, Sergio Mars and Ignacio Marín (2005). "Iterative Cluster Analysis of Protein Interaction Data". Bioinformatics 21: 364–378. doi:10.1093/bioinformatics/bti021. 
  4. ↑ (http://scholar.google.com/scholar?cites=5396059551679935817&as_sdt=2005&sciodt=0,5&hl=en)
  5. ↑ Tobias Fleck, Andrea Kappes, Dorothea Wagner (2013). "Graph Clustering with Surprise: Complexity and Exact Solutions". http://arxiv.org/abs/1310.6019. 
  6. ↑ Rodrigo Aldecoa and Ignacio Marín (2013). "SurpriseMe: an integrated tool for network community structure characterization using Surprise maximization". Bioinformatics in press. http://arxiv.org/abs/1310.2357. 
  7. ↑ M.E.J. Newman and M. Girvan (2004). "Finding and evaluating community structure in networks". Physical Review E 69 (2): 026113. doi:10.1103/PhysRevE.69.026113. 
  8. ↑ Santo Fortunato and Marc Barthélemy (2007). "Resolution limit in community detection". Proceedings of the National Academy of Sciences USA 104 (1): 36–41. doi:10.1073/pnas.0605965104. PMC 1765466. PMID 17190818. 
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.