Surjunctive group
| Is every group surjunctive? |
In mathematics, a surjunctive group is a group such that, for every cellular automaton with finite alphabet over the group, if no two states of the automaton have the same successor, then every state of the automaton has a unique predecessor. Surjunctive groups were introduced by Gottschalk (1973).
A cellular automaton consists of a regular system of cells, each containing a symbol from an alphabet, together with a uniform rule called a transition function for updating all cells simultaneously. Most commonly the cells are arranged in the form of an integer lattice, which can be modeled in group-theoretic terms as a free abelian group. However, it is possible to define a cellular automaton over an arbitrary group by letting the states of the automaton be mappings from the group to a finite set, and letting the state transition function of the automaton be a continuous function on the states that is equivariant with the group action; in this case, the Curtis–Hedlund–Lyndon theorem ensures that the transition function's value is determined by a finite neighborhood of each group element.
For the state transition function to be a surjective function, every state must have a predecessor (there can be no Garden of Eden), and for it to be an injective function, no two states may have the same successor. Thus, a group 
is surjunctive if, for every finite set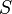 
, every continuous equivariant injective function 
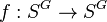is also surjective.[1] The implication from injectivity to surjectivity is a form of the Garden of Eden theorem, and the cellular automata defined from injective and surjective transition functions are reversible.
Examples of surjunctive groups include all locally residually finite groups,[2] all free groups,[2] all subgroups of surjunctive groups,[3] all abelian groups,[2] all sofic groups,[4] and every locally surjunctive group.[3] When he introduced surjunctive groups in 1973, Gottschalk observed that there were no known examples of non-surjunctive groups; as of 2010, it is still unknown whether every group is surjunctive.
See also
- Ax–Grothendieck theorem, an analogous result for polynomials
Notes
References
- Ceccherini-Silberstein, Tullio; Coornaert, Michel (2010), "Surjunctive groups", Cellular Automata and Groups, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, doi:10.1007/978-3-642-14034-1_3, ISBN 978-3-642-14033-4, MR 2683112, Zbl 1218.37004
- Gottschalk, Walter (1973), "Some general dynamical notions", Recent Advances in Topological Dynamics (Proc. Conf. Topological Dynamics, Yale Univ., New Haven, Conn., 1972; in honor of Gustav Arnold Hedlund), Lecture Notes in Math. 318, Berlin, New York: Springer-Verlag, pp. 120–125, doi:10.1007/BFb0061728, MR 0407821, Zbl 0255.54035