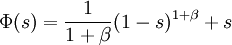Superprocess

From Wikipedia, the free encyclopedia

An 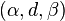$(\alpha ,d,\beta )$ -superprocess, $X(t,dx)$ , is a stochastic process on ${\mathbb {R}}\times {\mathbb {R}}^{d}$ that is usually constructed as a special limit of branching diffusion where the branching mechanism is given by its factorial moment generating function:

$\Phi (s)={\frac {1}{1+\beta }}(1-s)^{{1+\beta }}+s$

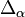and the spatial motion of individual particles is given by the $\alpha$ -symmetric stable process with infinitesimal generator $\Delta _{{\alpha }}$ .

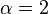The $\alpha =2$ case corresponds to standard Brownian motion and the 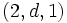$(2,d,1)$ -superprocess is called the Dawson-Watanabe superprocess or super-Brownian motion.

One of the most important properties of superprocesses is that they are intimately connected with certain nonlinear partial differential equations. The simplest such equation is

$\Delta u-u^{2}=0\ on\ {\mathbb {R}}^{d}.$

References

Eugene B. Dynkin (2004). Superdiffusions and positive solutions of nonlinear partial differential equations. Appendix A by J.-F. Le Gall and Appendix B by I. E. Verbitsky. University Lecture Series, 34. American Mathematical Society. ISBN 9780821836828.

Alison Etheridge (2000). An Introduction to Superprocesses. American Mathematical Society. ISBN 9780821827062.

v t e Stochastic processes

Discrete time	Bernoulli process Branching process Chinese restaurant process Galton–Watson process Independent and identically distributed random variables Markov chain Moran process Random walk Loop-erased Self-avoiding

Continuous time	Bessel process Birth–death process Brownian motion Bridge Excursion Fractional Geometric Meander Cauchy process Contact process Cox process Diffusion process Empirical process Feller process Fleming–Viot process Gamma process Hunt process Interacting particle systems Itō diffusion Itō process Jump diffusion Jump process Lévy process Local time Markov additive process McKean–Vlasov process Ornstein–Uhlenbeck process Poisson process Compound Non-homogeneous Point process Schramm–Loewner evolution Semimartingale Sigma-martingale Stable process Superprocess Telegraph process Variance gamma process Wiener process Wiener sausage

Both	Branching process Gaussian process Hidden Markov model (HMM) Markov process Martingale Differences Local Sub- Super- Random dynamical system Regenerative process Renewal process White noise

Fields and other	Dirichlet process Gaussian random field Gibbs measure Hopfield model Ising model Markov random field Percolation Pitman–Yor process Point process Cox Poisson Potts model Random field Random graph

Time series models	Autoregressive conditional heteroskedasticity (ARCH) model Autoregressive integrated moving average (ARIMA) model Autoregressive (AR) model Autoregressive–moving-average (ARMA) model Generalized autoregressive conditional heteroskedasticity (GARCH) model Moving-average (MA) model

Financial models	Black–Derman–Toy Black–Karasinski Black–Scholes Chen Constant elasticity of variance (CEV) Cox–Ingersoll–Ross (CIR) Garman–Kohlhagen Heath–Jarrow–Morton (HJM) Heston Ho–Lee Hull–White LIBOR market SABR volatility Vašícek

Actuarial models	Bühlmann Cramér–Lundberg Risk process Sparre–Anderson

Queueing models	Bulk Fluid Generalized queueing network M/G/1 M/M/1 M/M/c

Properties	Càdlàg paths Continuous Continuous paths Ergodic Exchangeable Feller-continuous Gauss–Markov Markov Mixing Piecewise deterministic Predictable Progressively measurable Self-similar Stationary Time-reversible

Limit theorems	Central limit theorem Donsker's theorem Doob's martingale convergence theorems Ergodic theorem Fisher–Tippett–Gnedenko theorem Large deviation principle Law of large numbers (weak/strong) Law of the iterated logarithm Maximal ergodic theorem Sanov's theorem

Inequalities	Burkholder–Davis–Gundy Doob's martingale Kunita–Watanabe

Tools	Cameron–Martin formula Convergence of random variables Doléans-Dade exponential Doob decomposition theorem Doob–Meyer decomposition theorem Doob's optional stopping theorem Dynkin's formula Feynman–Kac formula Filtration Girsanov theorem Infinitesimal generator Itō integral Itō's lemma Kolmogorov continuity theorem Kolmogorov extension theorem Lévy–Prokhorov metric Malliavin calculus Martingale representation theorem Optional stopping theorem Prohorov theorem Quadratic variation Reflection principle Skorokhod integral Skorokhod's representation theorem Skorokhod space Snell envelope Stochastic differential equation Tanaka Stopping time Stratonovich integral Uniform integrability Usual hypotheses Wiener space Classical Abstract

Disciplines	Actuarial mathematics Econometrics Ergodic theory Extreme value theory (EVT) Large deviations theory Mathematical finance Mathematical statistics Probability theory Queueing theory Renewal theory Ruin theory Statistics Stochastic analysis Time series analysis Machine learning

List of topics Category

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.