Superintegrable Hamiltonian system
In mathematics, a superintegrable Hamiltonian system is a Hamiltonian system on a 2n-dimensional symplectic manifold for which the following conditions hold:
(i) There exist n ≤ k independent integrals F i of motion. Their level surfaces (invariant submanifolds) form a fibered manifold 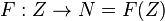 over a connected open subset
over a connected open subset  .
.
(ii) There exist smooth real functions  on
on  such that the Poisson bracket of integrals of motion reads
such that the Poisson bracket of integrals of motion reads
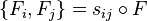 .
.
(iii) The matrix function  is of constant corank
is of constant corank 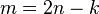 on
on  .
.
If 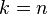 , this is the case of a completely integrable Hamiltonian system. The Mishchenko-Fomenko theorem for superintegrable Hamiltonian systems generalizes the Liouville-Arnold theorem on action-angle coordinates of completely integrable Hamiltonian system as follows.
, this is the case of a completely integrable Hamiltonian system. The Mishchenko-Fomenko theorem for superintegrable Hamiltonian systems generalizes the Liouville-Arnold theorem on action-angle coordinates of completely integrable Hamiltonian system as follows.
Let invariant submanifolds of a superintegrable Hamiltonian system be connected compact and mutually diffeomorphic. Then the fibered manifold  is a fiber bundle
in tori
is a fiber bundle
in tori  . Given its fiber
. Given its fiber  , there exists an open neighbourhood
, there exists an open neighbourhood  of
of  which is a trivial fiber bundle provided with the bundle (generalized action-angle) coordinates
which is a trivial fiber bundle provided with the bundle (generalized action-angle) coordinates 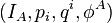 ,
,
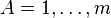 ,
,  such that
such that  are coordinates on
are coordinates on  . These coordinates are the Darboux coordinates on a symplectic manifold
. These coordinates are the Darboux coordinates on a symplectic manifold  . A Hamiltonian of a superintegrable system depends only on the action variables
. A Hamiltonian of a superintegrable system depends only on the action variables 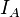 which are the Casimir functions of the coinduced Poisson structure on
which are the Casimir functions of the coinduced Poisson structure on  .
.
The Liouville-Arnold theorem for completely integrable systems and the Mishchenko-Fomenko theorem for the superintegrable ones are generalized to the case of non-compact invariant submanifolds. They are diffeomorphic to a toroidal cylinder 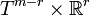 .
.
See also
References
- Mishchenko, A., Fomenko,A., Generalized Liouville method of integration of Hamiltonian systems, Funct. Anal. Appl. 12 (1978) 113.
- Bolsinov, A., Jovanovic, B., Noncommutative integrability, moment map and geodesic flows, Ann. Global Anal. Geom. 23 (2003) 305; arXiv:math-ph/0109031.
- Fasso, F., Superintegrable Hamiltonian systems: geometry and applications, Acta Appl. Math. 87(2005) 93.
- Fiorani, E., Sardanashvily, G., Global action-angle coordinates for completely integrable systems with non-compact invariant manifolds, J. Math. Phys. 48 (2007) 032901; arXiv:math/0610790.
- Giachetta, G., Mangiarotti, L., Sardanashvily, G., Geometric Methods in Classical and Quantum Mechanics (World Scientific, Singapore, 2010) ISBN 978-981-4313-72-8; arXiv: 1303.5363.