Supercompact cardinal
In set theory, a supercompact cardinal is a type of large cardinal. They display a variety of reflection properties.
Formal definition
If λ is any ordinal, κ is λ-supercompact means that there exists an elementary embedding j from the universe V into a transitive inner model M with critical point κ, j(κ)>λ and
That is, M contains all of its λ-sequences. Then κ is supercompact means that it is λ-supercompact for all ordinals λ.
Alternatively, an uncountable cardinal κ is supercompact if for every A such that |A| ≥ κ there exists a normal measure over [A]< κ.
[A]< κ is defined as follows:
Properties
Supercompact cardinals have reflection properties. If a cardinal with some property (say a 3-huge cardinal) that is witnessed by a structure of limited rank exists above a supercompact cardinal κ, then a cardinal with that property exists below κ. For example, if κ is supercompact and the Generalized Continuum Hypothesis holds below κ then it holds everywhere because a bijection between the powerset of ν and a cardinal at least ν++ would be a witness of limited rank for the failure of GCH at ν so it would also have to exist below κ.
Finding a canonical inner model for supercompact cardinals is one of the major problems of inner model theory.
References
- Drake, F. R. (1974). Set Theory: An Introduction to Large Cardinals (Studies in Logic and the Foundations of Mathematics ; V. 76). Elsevier Science Ltd. ISBN 0-444-10535-2.
- Jech, Thomas (2002). Set theory, third millennium edition (revised and expanded). Springer. ISBN 3-540-44085-2.
- Kanamori, Akihiro (2003). The Higher Infinite : Large Cardinals in Set Theory from Their Beginnings (2nd ed ed.). Springer. ISBN 3-540-00384-3.
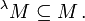
![[A]^{{<\kappa }}:=\{X\subseteq A||X|<\kappa \}\,.](/2014-wikipedia_en_all_02_2014/I/media/b/3/2/b/b32bcfd83ce207b2e9ba1e45a9c19b1f.png)