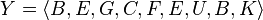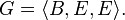Subsequence

From Wikipedia, the free encyclopedia

In mathematics, a subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements. For example, the sequence 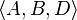\langle A,B,D\rangle is a subsequence of 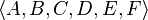\langle A,B,C,D,E,F\rangle . They should not be confused with substring which is a refinement of subsequence.

Common subsequence

Given two sequences X and Y, a sequence G is said to be a common subsequence of X and Y, if G is a subsequence of both X and Y. For example, if

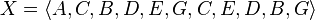X=\langle A,C,B,D,E,G,C,E,D,B,G\rangle and
Y=\langle B,E,G,C,F,E,U,B,K\rangle

then a common subsequence of X and Y could be

G=\langle B,E,E\rangle .

This would not be the longest common subsequence, since G only has length 3, and the common subsequence 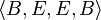\langle B,E,E,B\rangle has length 4. The longest common subsequence of X and Y is \langle B,E,G,C,E,B\rangle .

Applications

Subsequences have applications to computer science,[1] especially in the discipline of bioinformatics, where computers are used to compare, analyze, and store DNA strands.

Take two strands of DNA, say:

ORG1 = ACGGTGTCGTGCTATGCTGATGCTGACTTATATGCTA
and
ORG2 = CGTTCGGCTATCGTACGTTCTATTCTATGATTTCTAA.

Subsequences are used to determine how similar the two strands of DNA are, using the DNA bases: adenine, guanine, cytosine and thymine.

Theorems

  • Every infinite sequence of real numbers has an infinite monotone subsequence (This is a lemma used in the proof of the Bolzano–Weierstrass theorem).
  • Every bounded infinite sequence in Rn has a convergent subsequence (This is the Bolzano–Weierstrass theorem).
  • For every integers r and s, every finite sequence of length at least (r − 1)(s − 1) + 1 contains a monotonically increasing subsequence of length r or a monotonically decreasing subsequence of length s (This is the Erdős–Szekeres theorem).

See also

Notes

  1. ↑ In computer science, string is often used as a synonym for sequence, but it is important to note that substring and subsequence are not synonyms. Substrings are consecutive parts of a string, while subsequences need not be. This means that a substring of a string is always a subsequence of the string, but a subsequence of a string is not always a substring of the string, see: Gusfield, Dan (1999) [1997]. Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology. USA: Cambridge University Press. p. 4. ISBN 0-521-58519-8. 

This article incorporates material from subsequence on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.