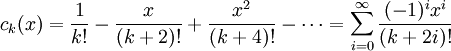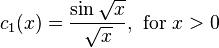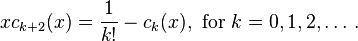Stumpff function

From Wikipedia, the free encyclopedia

In celestial mechanics, the Stumpff functions c_k(x), developed by Karl Stumpff, are used for analyzing orbits using the universal variable formulation.^[1] They are defined by the formula:

$c_{k}(x)={\frac {1}{k!}}-{\frac {x}{(k+2)!}}+{\frac {x^{2}}{(k+4)!}}-\cdots =\sum _{{i=0}}^{\infty }{{\frac {(-1)^{i}x^{i}}{(k+2i)!}}}$

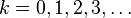for $k=0,1,2,3,\ldots$ The series above converges absolutely for all real x.

By comparing the Taylor series expansion of the trigonometric functions sin and cos with c₀(x) and c₁(x), a relationship can be found:

$c_{0}(x)=\cos {{\sqrt x}},{\text{ for }}x>0$

$c_{1}(x)={\frac {\sin {{\sqrt x}}}{{\sqrt x}}},{\text{ for }}x>0$

Similarly, by comparing with the expansion of the hyperbolic functions sinh and cosh we find:

$c_{0}(x)=\cosh {{\sqrt {-x}}},{\text{ for }}x<0$

$c_{1}(x)={\frac {\sinh {{\sqrt {-x}}}}{{\sqrt {-x}}}},{\text{ for }}x<0$

The Stumpff functions satisfy the recursive relations:

$xc_{{k+2}}(x)={\frac {1}{k!}}-c_{k}(x),{\text{ for }}k=0,1,2,\ldots \,.$

References

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.