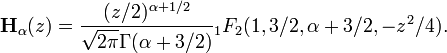Struve function
In mathematics, Struve functions  , are solutions y(x) of the non-homogenous Bessel's differential equation:
, are solutions y(x) of the non-homogenous Bessel's differential equation:
introduced by Hermann Struve (1882).
The complex number α is the order of the Struve function, and is often an integer.
The modified Struve functions 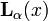 are equal to
are equal to
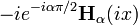 .
.
Definitions
Since this is a non-homogenous equation, solutions can be constructed from a single particular solution by adding the solutions of the homogeneous problem. In this case, the homogenous solutions are the Bessel functions, and the particular solution may be chosen as the corresponding Struve function.
Power series expansion
Struve functions, denoted as  have the following power series form
have the following power series form
where  is the gamma function.
is the gamma function.
The modified Struve function, denoted as 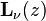 have the following power series form
have the following power series form
Integral form
Another definition of the Struve function, for values of α satisfying 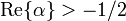 , is possible using an integral representation:
, is possible using an integral representation:
Asymptotic forms
For small x, the power series expansion is given above.
For large x, one obtains:
where 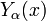 is the
Neumann function.
is the
Neumann function.
Properties
The Struve functions satisfy the following recurrence relations:
Relation to other functions
Struve functions of integer order can be expressed in terms of Weber functions En and vice versa: if n is a non-negative integer then
Struve functions of order n+1/2 (n an integer) can be expressed in terms of elementary functions. In particular if n is a non-negative integer then
where the right hand side is a spherical Bessel function.
Struve functions (of any order) can be expressed in terms of the generalized hypergeometric function 1F2 (which is not the Gauss hypergeometric function 2F1) :
References
- R.M. Aarts and Augustus J.E.M. Janssen (2003). "Approximation of the Struve function H1 occurring in impedance calculations". J. Acoust. Soc. Am. 113 (5): 2635–2637. Bibcode:2003ASAJ..113.2635A. doi:10.1121/1.1564019. PMID 12765381.
- Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 12", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, p. 496, ISBN 978-0486612720, MR 0167642.
- Ivanov, A.B. (2001), "S/s090700", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Paris, R. B. (2010), "Struve function", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248
- Struve, H. (1882). "Beitrag zur Theorie der Diffraction an Fernröhren". Ann. Physik Chemie 17 (13): 1008–1016. Bibcode:1882AnP...253.1008S. doi:10.1002/andp.18822531319.
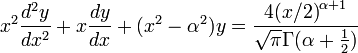

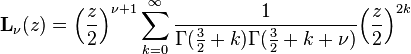
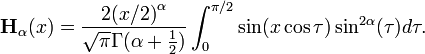
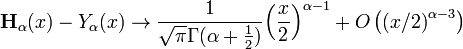
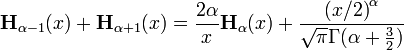
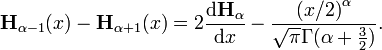
![{\mathbf {E}}_{n}(z)={\frac {1}{\pi }}\sum _{{k=0}}^{{[{\frac {n-1}{2}}]}}{\frac {\Gamma (k+1/2)(z/2)^{{n-2k-1}}}{\Gamma (n-1/2-k)}}{\mathbf {H}}_{n}](/2014-wikipedia_en_all_02_2014/I/media/1/9/5/4/19542d23b025acabdae67729f3d62ff8.png)
![{\mathbf {E}}_{{-n}}(z)={\frac {(-1)^{{n+1}}}{\pi }}\sum _{{k=0}}^{{[{\frac {n-1}{2}}]}}{\frac {\Gamma (n-k-1/2)(z/2)^{{-n+2k+1}}}{\Gamma (k+3/2)}}{\mathbf {H}}_{{-n}}.](/2014-wikipedia_en_all_02_2014/I/media/e/c/6/4/ec64b1f8ee489297f556e4a7a00247d0.png)