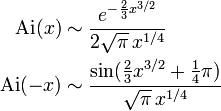Stokes line

From Wikipedia, the free encyclopedia

In complex analysis a Stokes line, named after Sir George Gabriel Stokes, is a line in the complex plane which 'turns on' different kinds of behaviour when one 'passes over' this line – although, somewhat confusingly, this definition is sometimes used for anti-Stokes lines. This article follows the former definition, more common in mathematical literature (but less common in physics literature). When approximating integral equations it is vital to know where the Stokes lines are so as to keep track of exponential smallness.

The Airy function

The Airy function Ai(x) is one of two solutions to a simple differential equation

y''-xy=0,\,

which it is often useful to approximate for many values of x – including complex values. If we regard the limit of x as large and real, and would like to approximate the Airy function for both positive and negative values, we would find that

{\begin{aligned}{\mathrm {Ai}}(x)&{}\sim {\frac {e^{{-{\frac 23}x^{{3/2}}}}}{2{\sqrt \pi }\,x^{{1/4}}}}\\{\mathrm {Ai}}(-x)&{}\sim {\frac {\sin({\frac 23}x^{{3/2}}+{\frac 14}\pi )}{{\sqrt \pi }\,x^{{1/4}}}}\\\end{aligned}}

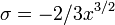which are two very different expressions. What has happened is that as we have increased the argument of x from 0 to pi (rotating it around through the upper half complex plane) we have crossed a Stokes line, which in this case is at \operatorname {arg}\,x=2\pi /3. A more thorough analysis is possible by defining a new variable \sigma =-2/3x^{{3/2}} with small argument – we find that exponentially small terms are 'turned on' via the erf function. These small terms then grow, and cause the oscillatory behaviour at arg x = π.

Optics

Stokes and anti-Stokes lines.
In the context of optics, a Stokes line refers to the radiation of particular wavelengths present in the line spectra associated with fluorescence and the Raman scattering. Stokes lines are of longer wavelength than that of the exciting radiation responsible for the fluorescence or Raman effect.

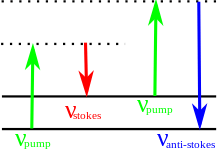
The energy of the scattered radiation is less than the incident radiation for the Stokes line and the energy of the scattered radiation is more than the incident radiation for the anti-Stokes line. The energy increase or decrease from the excitation is related to the vibrational energy spacing in the ground electronic state of the molecule and therefore the wavenumber of the Stokes and anti-Stokes lines are a direct measure of the vibrational energies of the molecule. The probability of anti-Stokes transition is much less than the Stokes transition as at room temperature majority of molecule is present in the lowest vibrational level.

See also

References

Witten, Ed (2010). "Analytic Continuation Of Chern-Simons Theory". arXiv:hep-th/1001.2933v4.


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.