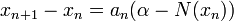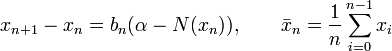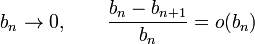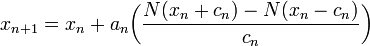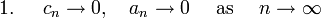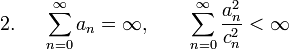Stochastic approximation
Stochastic approximation methods are a family of iterative stochastic optimization algorithms that attempt to find zeroes or extrema of functions which cannot be computed directly, but only estimated via noisy observations.
Mathematically, this refers to solving:
where the objective is to find the parameter 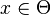 , which minimizes
, which minimizes  for some unknown random variable,
for some unknown random variable,  . Denoting
. Denoting  as the dimension of the parameter
as the dimension of the parameter  , we can assume that while the domain
, we can assume that while the domain 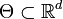 is known, the objective function,
is known, the objective function,  , cannot be computed exactly, but instead approximated via simulation. This can be intuitively explained as follows.
, cannot be computed exactly, but instead approximated via simulation. This can be intuitively explained as follows.  is the original function we want to minimize. However, due to noise,
is the original function we want to minimize. However, due to noise,  can not be evaluated exactly. This situation is modeled by the function
can not be evaluated exactly. This situation is modeled by the function 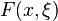 , where
, where  represents the noise and is a random variable. Since
represents the noise and is a random variable. Since  is a random variable, so is the value of
is a random variable, so is the value of 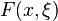 . The objective is then to minimize
. The objective is then to minimize  , but through evaluating
, but through evaluating 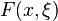 . A reasonable way to do this is to minimize the expectancy of
. A reasonable way to do this is to minimize the expectancy of 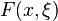 , i.e.,
, i.e., ![{\mathbb E}[F(x,\xi )]](/2014-wikipedia_en_all_02_2014/I/media/8/9/7/d/897df5916e39945f2c92a500f6ff5fd1.png) .
.
The first, and prototypical, algorithms of this kind are the Robbins-Monro and Kiefer-Wolfowitz algorithms.
Robbins–Monro algorithm
The Robbins–Monro algorithm, introduced in 1951 by Herbert Robbins and Sutton Monro,[1] presented a methodology for solving a root finding problem, where the function is represented as an expected value. Assume that we have a function  , and a constant
, and a constant  , such that the equation
, such that the equation 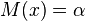 has a unique root at
has a unique root at 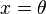 . It is assumed that while we cannot directly observe the function
. It is assumed that while we cannot directly observe the function  , we can instead obtain measurements of the random variable
, we can instead obtain measurements of the random variable  where
where ![{\mathbb E}[N(x)]=M(x)](/2014-wikipedia_en_all_02_2014/I/media/4/c/2/3/4c23fd5643e4e8868a75c06c944b2110.png) . The structure of the algorithm is to then generate iterates of the form:
. The structure of the algorithm is to then generate iterates of the form:
Here,  is a sequence of positive step sizes. Robbins and Monro proved [1], Theorem 2 that
is a sequence of positive step sizes. Robbins and Monro proved [1], Theorem 2 that  converges in
converges in 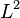 (and hence also in probability) to
(and hence also in probability) to 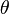 provided that:
provided that:
-
 is uniformly bounded,
is uniformly bounded, -
 is nondecreasing,
is nondecreasing, -
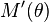 exists and is positive, and
exists and is positive, and - The sequence
 satisfies the following requirements:
satisfies the following requirements:
A particular sequence of steps which satisfy these conditions, and was suggested by Robbins–Monro, have the form:  , for
, for  . Other series are possible but in order to average out the noise in
. Other series are possible but in order to average out the noise in  , the above condition must be met.
, the above condition must be met.
Complexity results
- If
 is twice continuously differentiable, and strongly convex, and the minimizer of
is twice continuously differentiable, and strongly convex, and the minimizer of  belongs to the interior of
belongs to the interior of 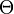 , then the Robbins-Monro algorithm will achieve the asymptotically optimal convergence rate, with respect to the objective function, being
, then the Robbins-Monro algorithm will achieve the asymptotically optimal convergence rate, with respect to the objective function, being ![{\mathbb E}[f(x_{n})-f^{*}]=O(1/n)](/2014-wikipedia_en_all_02_2014/I/media/6/e/8/8/6e88040db2410c6b09b021fc5be001eb.png) , where
, where 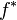 is the minimal value of
is the minimal value of  over
over 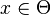 .[2][3]
.[2][3] - Conversely, in the general convex case, where we lack both the assumption of smoothness and strong convexity, Nemirovski and Yudin [4] have shown that the asymptotically optimal convergence rate, with respect to the objective function values, is
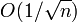 . They have also proven that this rate cannot be improved.
. They have also proven that this rate cannot be improved.
Subsequent developments
While the Robbins-Monro algorithm is theoretically able to achieve  under the assumption of twice continuous differentiability and strong convexity, it can perform quite poorly upon implementation. This is primarily due to the fact that the algorithm is very sensitive to the choice of the step size sequence, and the supposed asymptotically optimal step size policy can be quite harmful in the beginning.[3][5]
under the assumption of twice continuous differentiability and strong convexity, it can perform quite poorly upon implementation. This is primarily due to the fact that the algorithm is very sensitive to the choice of the step size sequence, and the supposed asymptotically optimal step size policy can be quite harmful in the beginning.[3][5]
To overcome this shortfall, Polyak and Juditsky,[6] presented a method of accelerating Robbins-Monro through the use of longer steps, and averaging of the iterates. The algorithm would have the following structure:
The convergence of 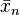 to the unique root
to the unique root 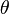 relies on the condition that the step sequence
relies on the condition that the step sequence 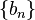 decreases sufficiently slowly. That is
decreases sufficiently slowly. That is
Therefore, the sequence 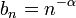 with
with  satisfies this restriction, but
satisfies this restriction, but 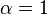 does not, hence the longer steps. Under the assumptions outlined in the Robbins-Monro algorithm, the resulting modification will result in the same asymptotically optimal convergence rate
does not, hence the longer steps. Under the assumptions outlined in the Robbins-Monro algorithm, the resulting modification will result in the same asymptotically optimal convergence rate  yet with a more robust step size policy.[6]
yet with a more robust step size policy.[6]
Prior to this, the idea of using longer steps and averaging the iterates had already been proposed by Nemirovski and Yudin [7] for the cases of solving the stochastic optimization problem with continuous convex objectives and for convex-concave saddle point problems. These algorithms were observed to attain the nonasymptotic rate 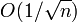 .
.
Kiefer-Wolfowitz algorithm
The Kiefer-Wolfowitz algorithm,[8] was introduced in 1952, and was motivated by the publication of the Robbins-Monro algorithm. However, the algorithm was presented as a method which would stochastically estimate the maximum of a function. Let  be a function which has a maximum at the point
be a function which has a maximum at the point 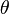 . It is assumed that
. It is assumed that  is unknown, however, certain observations
is unknown, however, certain observations  , where
, where ![{\mathbb E}[N(x)]=M(x)](/2014-wikipedia_en_all_02_2014/I/media/4/c/2/3/4c23fd5643e4e8868a75c06c944b2110.png) , can be made at any point
, can be made at any point  . The structure of the algorithm follows a gradient-like method, with the iterates being generated as follows:
. The structure of the algorithm follows a gradient-like method, with the iterates being generated as follows:
where the gradient of  is approximated using finite differences. The sequence
is approximated using finite differences. The sequence 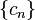 specifies the sequence of finite difference widths used for the gradient approximation, while the sequence
specifies the sequence of finite difference widths used for the gradient approximation, while the sequence 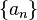 specifies a sequence of positive step sizes taken along that direction. Kiefer and Wolfowitz proved that, if
specifies a sequence of positive step sizes taken along that direction. Kiefer and Wolfowitz proved that, if  satisfied certain regularity conditions, then
satisfied certain regularity conditions, then  will converge to
will converge to 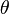 provided that:
provided that:
- The function
 has a unique point of maximum (minimum) and is strong concave (convex)
has a unique point of maximum (minimum) and is strong concave (convex)
- The algorithm was first presented with the requirement that the function
 maintains strong global convexity (concavity) over the entire feasible space. Given this condition is too restrictive to impose over the entire domain, Kiefer and Wolfowitz proposed that it is sufficient to impose the condition over a compact set
maintains strong global convexity (concavity) over the entire feasible space. Given this condition is too restrictive to impose over the entire domain, Kiefer and Wolfowitz proposed that it is sufficient to impose the condition over a compact set 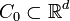 which is known to include the optimal solution.
which is known to include the optimal solution.
- The algorithm was first presented with the requirement that the function
- The selected sequences
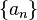 and
and 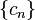 must be infinite sequences of positive numbers such that:
must be infinite sequences of positive numbers such that:
A suitable choice of sequences, as recommended by Kiefer and Wolfowitz, would be  and
and 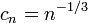 .
.
Subsequent developments and important issues
- The Kiefer Wolfowitz algorithm requires that for each gradient computation, at least
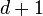 different parameter values must be simulated for every iteration of the algorithm, where
different parameter values must be simulated for every iteration of the algorithm, where  is the dimension of the search space. This means that when
is the dimension of the search space. This means that when  is large, the Kiefer-Wolfowitz algorithm will require substantial computational effort per iteration, leading to slow convergence.
is large, the Kiefer-Wolfowitz algorithm will require substantial computational effort per iteration, leading to slow convergence.
- To address this problem, Spall, proposed the use of simultaneous perturbations to estimate the gradient. This method would require only two simulations per iteration, regardless of the dimension
 .[9]
.[9]
- To address this problem, Spall, proposed the use of simultaneous perturbations to estimate the gradient. This method would require only two simulations per iteration, regardless of the dimension
- In the conditions required for convergence, the ability to specify a predetermined compact set that fulfills strong convexity (or concavity) and contains the unique solution can be difficult to find. With respect to real world applications, if the domain is quite large, these assumptions can be fairly restrictive and highly unrealistic.
Further developments
An extensive theoretical literature has grown up around these algorithms, concerning conditions for convergence, rates of convergence, multivariate and other generalizations, proper choice of step size, possible noise models, and so on.[10][11] These methods are also applied in control theory, in which case the unknown function which we wish to optimize or find the zero of may vary in time. In this case, the step size  should not converge to zero but should be chosen so as to track the function.[10], 2nd ed., chapter 3
should not converge to zero but should be chosen so as to track the function.[10], 2nd ed., chapter 3
C. Johan Masreliez and R. Douglas Martin were the first to apply stochastic approximation to robust estimation.[12]
See also
- Stochastic gradient descent
- Stochastic optimization
- Simultaneous perturbation stochastic approximation
References
- ↑ 1.0 1.1 Robbins, H.; Monro, S. (1951). "A Stochastic Approximation Method". The Annals of Mathematical Statistics 22 (3): 400. doi:10.1214/aoms/1177729586.
- ↑ Sacks, J. (1958). "Asymptotic Distribution of Stochastic Approximation Procedures". The Annals of Mathematical Statistics 29 (2): 373. doi:10.1214/aoms/1177706619. JSTOR 2237335.
- ↑ 3.0 3.1 Nemirovski, A.; Juditsky, A.; Lan, G.; Shapiro, A. (2009). "Robust Stochastic Approximation Approach to Stochastic Programming". SIAM Journal on Optimization 19 (4): 1574. doi:10.1137/070704277.
- ↑ Problem Complexity and Method Efficiency in Optimization, A. Nemirovski and D. Yudin, Wiley -Intersci. Ser. Discrete Math 15 John Wiley New York (1983) .
- ↑ Introduction to Stochastic Search and Optimization: Estimation, Simulation and Control, J.C. Spall, John Wiley Hoboken, NJ, (2003).
- ↑ 6.0 6.1 Polyak, B. T.; Juditsky, A. B. (1992). "Acceleration of Stochastic Approximation by Averaging". SIAM Journal on Control and Optimization 30 (4): 838. doi:10.1137/0330046.
- ↑ On Cezari's convergence of the steepest descent method for approximating saddle points of convex-concave functions, A. Nemirovski and D. Yudin, Dokl. Akad. Nauk SSR 2939, (1978 (Russian)), Soviet Math. Dokl. 19 (1978 (English)).
- ↑ Kiefer, J.; Wolfowitz, J. (1952). "Stochastic Estimation of the Maximum of a Regression Function". The Annals of Mathematical Statistics 23 (3): 462. doi:10.1214/aoms/1177729392.
- ↑ Spall, J. C. (2000). "Adaptive stochastic approximation by the simultaneous perturbation method". IEEE Transactions on Automatic Control 45 (10): 1839. doi:10.1109/TAC.2000.880982.
- ↑ 10.0 10.1 Kushner, H. J.; Yin, G. G. (1997). Stochastic Approximation Algorithms and Applications. doi:10.1007/978-1-4899-2696-8. ISBN 978-1-4899-2698-2.
- ↑ Stochastic Approximation and Recursive Estimation, Mikhail Borisovich Nevel'son and Rafail Zalmanovich Has'minskiĭ, translated by Israel Program for Scientific Translations and B. Silver, Providence, RI: American Mathematical Society, 1973, 1976. ISBN 0-8218-1597-0.
- ↑ Martin, R.; Masreliez, C. (1975). "Robust estimation via stochastic approximation". IEEE Transactions on Information Theory 21 (3): 263. doi:10.1109/TIT.1975.1055386.
![\min _{{x\in \Theta }}\;f(x)={\mathbb E}[F(x,\xi )]](/2014-wikipedia_en_all_02_2014/I/media/2/9/7/7/2977fbf0ae9bc6664473c6ea4fabf91d.png)