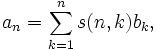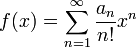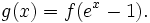Stirling transform
In combinatorial mathematics, the Stirling transform of a sequence { an : n = 1, 2, 3, ... } of numbers is the sequence { bn : n = 1, 2, 3, ... } given by
where 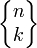 is the Stirling number of the second kind, also denoted S(n,k) (with a capital S), which is the number of partitions of a set of size n into k parts.
is the Stirling number of the second kind, also denoted S(n,k) (with a capital S), which is the number of partitions of a set of size n into k parts.
The inverse transform is
where s(n,k) (with a lower-case s) is a Stirling number of the first kind.
Berstein and Sloane (cited below) state "If an is the number of objects in some class with points labeled 1, 2, ..., n (with all labels distinct, i.e. ordinary labeled structures), then bn is the number of objects with points labeled 1, 2, ..., n (with repetitions allowed)."
If
is a formal power series (note that the lower bound of summation is 1, not 0), and
with an and bn as above, then
See also
References
- Bernstein, M.; Sloane, N. J. A. (1995). "Some canonical sequences of integers". Linear Algebra and its Applications. 226/228: 57–72. doi:10.1016/0024-3795(94)00245-9..