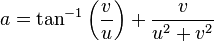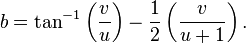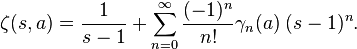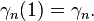Stieltjes constants
In mathematics, the Stieltjes constants are the numbers 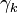 that occur in the Laurent series expansion of the Riemann zeta function:
that occur in the Laurent series expansion of the Riemann zeta function:
The zero'th constant  is known as the Euler–Mascheroni constant.
is known as the Euler–Mascheroni constant.
Representations
The Stieltjes constants are given by the limit
(In the case n = 0, the first summand requires evaluation of 00, which is taken to be 1.)
Cauchy's differentiation formula leads to the integral representation
Several representations in terms of integrals and infinite series are given in the papers of Coffey.
Numerical values
The first few values are:
n approximate value of γn OEIS 0 +0.5772156649015328606065120900824024310421593359 A001620 1 −0.0728158454836767248605863758749013191377363383 A082633 2 −0.0096903631928723184845303860352125293590658061 A086279 3 +0.0020538344203033458661600465427533842857158044 A086280 4 +0.0023253700654673000574681701775260680009044694 A086281 5 +0.0007933238173010627017533348774444448307315394 A086282 6 −0.0002387693454301996098724218419080042777837151 A183141 7 −0.0005272895670577510460740975054788582819962534 A183167 8 −0.0003521233538030395096020521650012087417291805 A183206 9 −0.0000343947744180880481779146237982273906207895 A184853 10 +0.0002053328149090647946837222892370653029598537 A184854 100 −4.2534015717080269623144385197278358247028931053 × 1017 1000 −1.5709538442047449345494023425120825242380299554 × 10486 10000 −2.2104970567221060862971082857536501900234397174 × 106883 100000 +1.9919273063125410956582272431568589205211659777 × 1083432
For large n, the Stieltjes constants grow rapidly in absolute value, and change signs in a complex pattern.
Numerical values of the Stieltjes constants up to n = 100000, accurate to over 10000 digits each, have been computed by Johansson. The numerical values can be retrieved from the LMFDB .
Asymptotic growth
The Stieltjes constants satisfy the bound
as proved by Berndt. A much tighter bound, valid for  , is given by Matsuoka:
, is given by Matsuoka:
Knessl and Coffey give a formula that approximates the Stieltjes constants accurately for large n. If v is the unique solution of
with  , and if
, and if  , then
, then
where
Up to 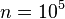 , the Knessl-Coffey approximation correctly predicts the sign of
, the Knessl-Coffey approximation correctly predicts the sign of 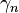 with the single exception of
with the single exception of  .
.
Generalized Stieltjes constants
More generally, one can define Stieltjes constants 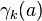 that occur in the Laurent series expansion of the Hurwitz zeta function:
that occur in the Laurent series expansion of the Hurwitz zeta function:
Here a is a complex number with Re(a)>0. Since the Hurwitz zeta function is a generalization of the Riemann zeta function, we have
References
- Weisstein, Eric W., "Stieltjes Constants", MathWorld.
- Plouffe, Simon. "Stieltjes Constants, from 0 to 78, 256 digits each".
- Kreminski, Rick (2003). "Newton-Cotes integration for approximating Stieltjes generalized Euler constants". Mathematics of Computation 72 (243): 1379–1397. doi:10.1090/S0025-5718-02-01483-7. MR 1972742.
- Coffey, Mark W. (2009). "Series representations for the Stieltjes constants". arXiv:0905.1111.
- Coffey, Mark W. (2010). "Addison-type series representation for the Stieltjes constants". J. Number Theory 130: 2049–2064. doi:10.1016/j.jnt.2010.01.003. MR 2653214.
- Knessl, Charles; Coffey, Mark W. (2011). "An effective asymptotic formula for the Stieltjes constants". Math. Comp. 80 (273): 379–386. doi:10.1090/S0025-5718-2010-02390-7. MR 2728984.
- Johansson, Fredrik (2013). "Rigorous high-precision computation of the Hurwitz zeta function and its derivatives". arXiv:1309.2877.
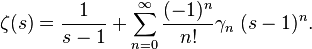

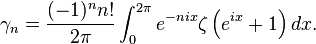


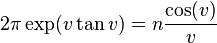

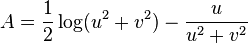
![B={\frac {2{\sqrt {2\pi }}{\sqrt {u^{2}+v^{2}}}}{[(u+1)^{2}+v^{2}]^{{1/4}}}}](/2014-wikipedia_en_all_02_2014/I/media/2/0/c/b/20cb691f31babf736862c4f85ef3d794.png)