Steve Jackson (mathematician)

From Wikipedia, the free encyclopedia

Steve Jackson (full name: Stephen Craig Jackson) is a set theorist at University of North Texas. Much of his most notable work has involved the descriptive set-theoretic consequences of the axiom of determinacy. In particular he is known for having calculated the values of all the projective ordinals (the suprema of the lengths of all prewellorderings of the reals at a particular level in the projective hierarchy) under the assumption that the axiom of determinacy holds.

In recent years he has also made contributions to the theory of Borel equivalence relations. With Dan Mauldin he solved the Steinhaus lattice problem.

Jackson earned his Ph.D. in 1983 at UCLA under the direction of Donald A. Martin, with a dissertation on A Calculation of δ¹₅. In it, he proved that, under AD,

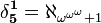
${\mathbf {\delta _{5}^{1}}}=\aleph _{{\omega ^{{\omega ^{{\omega }}}}+1}}$

thereby solving the first Victoria Delfino problem, one of the notorious problems of the combinatorics of the axiom of determinacy.

External links

Persondata
Name	Jackson, Steve
Alternative names
Short description	American mathematician
Date of birth
Place of birth
Date of death
Place of death

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.