Steriruncitruncated tesseractic honeycomb
From Wikipedia, the free encyclopedia
| Steriruncitruncated tesseractic honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform honeycomb |
| Schläfli symbol | t0,1,3,4{4,3,3,4} |
| Coxeter-Dynkin diagrams | |
| 4-face type | Runcitruncated tesseract truncated cubic prism 8-8 duoprism |
| Cell type | Cuboctahedron Truncated cube Triangular prism Octagonal prism |
| Face type | {3}, {4}, {8} |
| Vertex figure | Antialigned rectangular double pyramid |
| Coxeter groups | 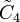 ×2, [[4,3,3,4]] ×2, [[4,3,3,4]] |
| Properties | Vertex transitive |
In four-dimensional Euclidean geometry, the steriruncitruncated tesseractic honeycomb is a uniform space-filling honeycomb.
Alternate names
- Celliprismatotruncated tesseractic tetracomb
- Great tomocubic-diprismatotesseractic tetracomb
Related honeycombs
The [4,3,3,4], ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , Coxeter group generates 31 permutations of uniform tessellations, 21 with distinct symmetry and 20 with distinct geometry. The expanded tesseractic honeycomb (also known as the stericated tesseractic honeycomb) is geometrically identical to the tesseractic honeycomb. Three of the symmetric honeycombs are shared in the [3,4,3,3] family. Two alternations (13) and (17), and the quarter tesseractic (2) are repeated in other families.
, Coxeter group generates 31 permutations of uniform tessellations, 21 with distinct symmetry and 20 with distinct geometry. The expanded tesseractic honeycomb (also known as the stericated tesseractic honeycomb) is geometrically identical to the tesseractic honeycomb. Three of the symmetric honeycombs are shared in the [3,4,3,3] family. Two alternations (13) and (17), and the quarter tesseractic (2) are repeated in other families.
| Extended symmetry |
Extended diagram |
Order | Honeycombs |
|---|---|---|---|
| [4,3,3,4]: | ×1 | ||
| [[4,3,3,4]] | ×2 | ||
| [(3,3)[1+,4,3,3,4,1+]] = [(3,3)[31,1,1,1]] = [3,4,3,3] |
= = |
×6 |
See also
Regular and uniform honeycombs in 4-space:
- Tesseractic honeycomb
- 16-cell honeycomb
- 24-cell honeycomb
- Truncated 24-cell honeycomb
- Snub 24-cell honeycomb
- 5-cell honeycomb
- Truncated 5-cell honeycomb
- Omnitruncated 5-cell honeycomb
References
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 p. 296, Table II: Regular honeycombs
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
- Richard Klitzing, 4D, Euclidean tesselations x4x3o3x4x - captatit - O102
| Fundamental convex regular and uniform honeycombs in dimensions 2–11 | |||||
|---|---|---|---|---|---|
| Family |  |
 |
 |
 |
 / /  / / 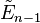 |
| Uniform tiling | {3[3]} | δ3 | hδ3 | qδ3 | Hexagonal |
| Uniform convex honeycomb | {3[4]} | δ4 | hδ4 | qδ4 | |
| Uniform 5-honeycomb | {3[5]} | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| Uniform 6-honeycomb | {3[6]} | δ6 | hδ6 | qδ6 | |
| Uniform 7-honeycomb | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| Uniform 8-honeycomb | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| Uniform 9-honeycomb | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| Uniform n-honeycomb | {3[n]} | δn | hδn | qδn | 1k2 • 2k1 • k21 |
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.