Steric tesseractic honeycomb
From Wikipedia, the free encyclopedia
| Steric tesseractic honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform honeycomb |
| Schläfli symbol | h4{4,3,3,4} |
| Coxeter-Dynkin diagram | |
| 4-face type | {4,3,3} t0,3{4,3,3} {3,3,4} {3,3}×{} |
| Cell type | {4,3} {3,3} {3}×{} |
| Face type | {4} {3} |
| Vertex figure | |
| Coxeter group | 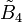 = [4,3,31,1] = [4,3,31,1] |
| Dual | ? |
| Properties | vertex-transitive |
In four-dimensional Euclidean geometry, the steric tesseractic honeycomb is a uniform space-filling tessellation (or honeycomb) in Euclidean 4-space.
Alternate names
- Small diprismatodemitesseractic tetracomb (siphatit)
Related honeycombs
The [4,3,31,1], ![]()
![]()
![]()
![]()
![]()
![]()
![]() , Coxeter group generates 31 permutations of uniform tessellations, 23 with distinct symmetry and 4 with distinct geometry. There are two alternated forms: the alternations (19) and (24) have the same geometry as the 16-cell honeycomb and snub 24-cell honeycomb respectively.
, Coxeter group generates 31 permutations of uniform tessellations, 23 with distinct symmetry and 4 with distinct geometry. There are two alternated forms: the alternations (19) and (24) have the same geometry as the 16-cell honeycomb and snub 24-cell honeycomb respectively.
| Extended symmetry |
Extended diagram |
Order | Honeycombs |
|---|---|---|---|
| [4,3,31,1]: | ×1 | ||
| <[4,3,31,1]>: =[4,3,3,4] |
= |
×2 | |
| [3[1+,4,3,31,1]] = [3[3,31,1,1]] = [3,3,4,3] |
= = |
×3 | |
| [(3,3)[1+,4,3,31,1]] = [(3,3)[31,1,1,1]] = [3,4,3,3] |
= = |
×12 |
See also
Regular and uniform honeycombs in 4-space:
- Tesseractic honeycomb
- 16-cell honeycomb
- 24-cell honeycomb
- Rectified 24-cell honeycomb
- Truncated 24-cell honeycomb
- Snub 24-cell honeycomb
- 5-cell honeycomb
- Truncated 5-cell honeycomb
- Omnitruncated 5-cell honeycomb
Notes
References
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
- Richard Klitzing, 4D, Euclidean tesselations x3o3o *b3o4x - siphatit - O108
| Fundamental convex regular and uniform honeycombs in dimensions 2–11 | |||||
|---|---|---|---|---|---|
| Family |  |
 |
 |
 |
 / /  / / 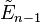 |
| Uniform tiling | {3[3]} | δ3 | hδ3 | qδ3 | Hexagonal |
| Uniform convex honeycomb | {3[4]} | δ4 | hδ4 | qδ4 | |
| Uniform 5-honeycomb | {3[5]} | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| Uniform 6-honeycomb | {3[6]} | δ6 | hδ6 | qδ6 | |
| Uniform 7-honeycomb | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| Uniform 8-honeycomb | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| Uniform 9-honeycomb | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| Uniform n-honeycomb | {3[n]} | δn | hδn | qδn | 1k2 • 2k1 • k21 |
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.