Stellar parallax

From Wikipedia, the free encyclopedia
Stellar parallax motion from annual parallax
Stellar parallax is the basis for the parsec, which is the distance from the Sun to an astronomical object which has a parallax angle of one arcsecond. (1 AU and 1 pc are not to scale, 1 pc = ~206265 AU)

Stellar parallax is the effect of parallax on distant stars in astronomy. It is parallax on an interstellar scale, and it can be used to determine the distance of Earth to another star directly with accurate astrometry. It was the subject of much debate in astronomy for hundreds of years, but was so difficult it was only achieved for a few of the nearest stars in the early 19th century. Even in the 21st century, stars with parallax measurements are relatively close on a galactic scale, and most distance measurements are calculated by red-shift or other methods.

The parallax is usually created by the different orbital positions of the Earth, which causes nearby stars to appear to move relative to more distant stars. By observing parallax, measuring angles and using geometry, one can determine the distance to various objects in space, typically stars, although other objects in space could be used.

Because other stars are far away, the angle for measurement is small and the skinny triangle approximation can be applied, the distance to an object (measured in parsecs) is the reciprocal of the parallax (measured in arcseconds): 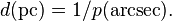d({\mathrm {pc}})=1/p({\mathrm {arcsec}}). For example, the distance to Proxima Centauri is 1/0.7687=1.3009 parsecs (4.243 ly).[1] The first successful measurement of stellar parallax was made by Friedrich Bessel in 1838 for the star 61 Cygni using a Fraunhofer heliometer at Königsberg Observatory.[2][3]

Early theory and attempts

Stellar parallax is so small (as to be unobservable until the 19th century) that it was used as a scientific argument against heliocentrism during the early modern age. It is clear from Euclid's geometry that the effect would be undetectable if the stars were far enough away, but for various reasons such gigantic distances involved seemed entirely implausible: it was one of Tycho Brahe's principal objections to Copernican heliocentrism that in order for it to be compatible with the lack of observable stellar parallax, there would have to be an enormous and unlikely void between the orbit of Saturn and the eighth sphere (the fixed stars).[4]

James Bradley first tried to measure stellar parallaxes in 1729. The stellar movement proved too insignificant for his telescope, but he instead discovered the aberration of light,[5] the nutation of the Earth’s axis, and did a cataloging of 3222 stars.

19th and 20th centuries

Bessel's heliometer

Stellar parallax is most often measured using annual parallax, defined as the difference in position of a star as seen from the Earth and Sun, i. e. the angle subtended at a star by the mean radius of the Earth's orbit around the Sun. The parsec (3.26 light-years) is defined as the distance for which the annual parallax is 1 arcsecond. Annual parallax is normally measured by observing the position of a star at different times of the year as the Earth moves through its orbit. Measurement of annual parallax was the first reliable way to determine the distances to the closest stars. The first successful measurements of stellar parallax were made by Friedrich Bessel in 1838 for the star 61 Cygni using a heliometer.[2][6]

Being very difficult to measure, only about 60 stellar parallaxes had been obtained by the end of the 19th century, mostly by use of the filar micrometer. Astrographs using astronomical photographic plates sped the process in the early 20th century. Automated plate-measuring machines[7] and more sophisticated computer technology of the 1960s allowed more efficient compilation of star catalogues. In the 1980s, charge-coupled devices (CCDs) replaced photographic plates and reduced optical uncertainties to one milliarcsecond.

Stellar parallax remains the standard for calibrating other measurement methods (see Cosmic distance ladder). Accurate calculations of distance based on stellar parallax require a measurement of the distance from the Earth to the Sun, now based on radar reflection off the surfaces of planets.[8]

The angles involved in these calculations are very small and thus difficult to measure. The nearest star to the Sun (and thus the star with the largest parallax), Proxima Centauri, has a parallax of 0.7687 ± 0.0003 arcsec.[1] This angle is approximately that subtended by an object 2 centimeters in diameter located 5.3 kilometers away.

Space astrometry for parallax

In 1989 the satellite Hipparcos was launched primarily for obtaining parallaxes and proper motions of nearby stars, increasing the reach of the method tenfold. Even so, Hipparcos is only able to measure parallax angles for stars up to about 1,600 light-years away, a little more than one percent of the diameter of the Milky Way Galaxy. The European Space Agency's Gaia mission, launched 19 December 2013, will be able to measure parallax angles to an accuracy of 10 microarcseconds, thus mapping nearby stars (and potentially planets) up to a distance of tens of thousands of light-years from earth.[9]

Other baselines

The motion of the Sun through space provides a longer baseline that will increase the accuracy of parallax measurements, known as secular parallax. For stars in the Milky Way disk, this corresponds to a mean baseline of 4 A.U. per year, while for halo stars the baseline is 40 A.U. per year. After several decades, the baseline can be orders of magnitude greater than the Earth-Sun baseline used for traditional parallax. However, secular parallax introduces a higher level of uncertainty because the relative velocity of other stars is an additional unknown. When applied to samples of multiple stars, the uncertainty can be reduced; the precision is inversely proportional to the square root of the sample size.[10]

Other parallax in astronomy

Other uses of the term parallax in astronomy, with different meanings are the Photometric parallax method, Spectroscopic parallax, and Dynamical parallax.

See also

References

  1. ↑ 1.0 1.1 Benedict, G. Fritz et al. (1999). "Interferometric Astrometry of Proxima Centauri and Barnard's Star Using HUBBLE SPACE TELESCOPE Fine Guidance Sensor 3: Detection Limits for Substellar Companions". The Astronomical Journal 118 (2): 1086–1100. arXiv:astro-ph/9905318. Bibcode:1999astro.ph..5318B. doi:10.1086/300975. 
  2. ↑ 2.0 2.1 Zeilik & Gregory 1998, p. 44.
  3. ↑ Alan W. Hirshfeld - Parallax: The Race to Measure the Cosmos (2002) - Page 259, Google Books 2010
  4. ↑ See p.51 in The reception of Copernicus' heliocentric theory: proceedings of a symposium organized by the Nicolas Copernicus Committee of the International Union of the History and Philosophy of Science, Torun, Poland, 1973, ed. Jerzy Dobrzycki, International Union of the History and Philosophy of Science. Nicolas Copernicus Committee; ISBN 90-277-0311-6, ISBN 978-90-277-0311-8
  5. ↑ Robert K. Buchheim - The sky is your laboratory: advanced astronomy projects for amateurs(2007) - Page 184, Google Books 2010
  6. ↑ Bessel, FW, "Bestimmung der Entfernung des 61sten Sterns des Schwans" (1838) Astronomische Nachrichten, vol. 16, pp. 65-96.
  7. ↑ CERN paper on plate measuring machine USNO StarScan
  8. ↑ Zeilik & Gregory 1998, § 22-3.
  9. ↑ Henney, Paul J. "ESA's Gaia Mission to study stars". Astronomy Today. Retrieved 2008-03-08. 
  10. ↑ Popowski, Piotr; Gould, Andrew (1998-01-29). "Mathematics of Statistical Parallax and the Local Distance Scale". arXiv:astro-ph/9703140 [astro-ph].
  • Hirshfeld, Alan w. (2001). Parallax: The Race to Measure the Cosmos. New York: W. H. Freeman. ISBN 0-7167-3711-6 
  • Whipple, Fred L. (2007). Earth Moon and Planets. Read Books. ISBN 1-4067-6413-2 .
  • Zeilik, Michael A.; Gregory, Stephan A. (1998). Introductory Astronomy & Astrophysics (4th ed.). Saunders College Publishing. ISBN 0-03-006228-4 .

Further reading

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.