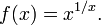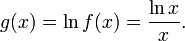Steiner's problem
From Wikipedia, the free encyclopedia
Steiner's problem is the problem of finding the maximum of the function
It is named after Jakob Steiner.
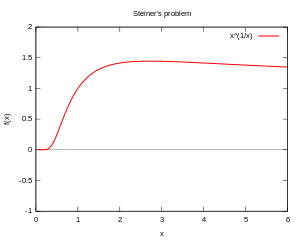
The maximum is at  , where e denotes the base of natural logarithms. One can determine that by solving the equivalent problem of maximizing
, where e denotes the base of natural logarithms. One can determine that by solving the equivalent problem of maximizing
The derivative of 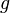 can be calculated to be
can be calculated to be
It follows that  is positive for
is positive for 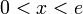 and negative for
and negative for  , which implies that
, which implies that 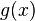 (and therefore
(and therefore  ) increases for
) increases for 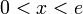 and decreases for
and decreases for  Thus,
Thus,  is the unique global maximum of
is the unique global maximum of 
References
- ↑ Eric W. Weisstein. "Steiner's Problem". MathWorld. Retrieved 12/08/2010.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.