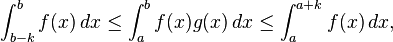Steffensen's inequality

From Wikipedia, the free encyclopedia

In mathematics, Steffensen's inequality, named after Johan Frederik Steffensen, is an integral inequality in real analysis. It states that if ƒ : [a, b] → R is a non-negative, monotonically decreasing, integrable function and g : [a, b] → [0, 1] is another integrable function, then

$\int _{{b-k}}^{{b}}f(x)\,dx\leq \int _{{a}}^{{b}}f(x)g(x)\,dx\leq \int _{{a}}^{{a+k}}f(x)\,dx,$

where

$k=\int _{{a}}^{{b}}g(x)\,dx.$

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.