Static spacetime

From Wikipedia, the free encyclopedia

In general relativity, a spacetime is said to be static if it admits a global, non-vanishing, timelike Killing vector field $K$ which is irrotational, i.e., whose orthogonal distribution is involutive. (Note that the leaves of the associated foliation are necessarily space-like hypersurfaces.) Thus, a static spacetime is a stationary spacetime satisfying this additional integrability condition. These spacetimes form one of the simplest classes of Lorentzian manifolds.

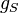Locally, every static spacetime looks like a standard static spacetime which is a Lorentzian warped product R $\times$ S with a metric of the form $g[(t,x)]=-\beta (x)dt^{{2}}+g_{{S}}[x]$ , where R is the real line, $g_{{S}}$ is a (positive definite) metric and $\beta$ is a positive function on the Riemannian manifold S.

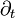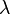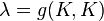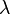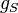In such a local coordinate representation the Killing field $K$ may be identified with $\partial _{t}$ and S, the manifold of $K$ -trajectories, may be regarded as the instantaneous 3-space of stationary observers. If $\lambda$ is the square of the norm of the Killing vector field, $\lambda =g(K,K)$ , both $\lambda$ and $g_{S}$ are independent of time (in fact $\lambda =-\beta (x)$ ). It is from the latter fact that a static spacetime obtains its name, as the geometry of the space-like slice S does not change over time.

Examples of static spacetimes

The (exterior) Schwarzschild solution
de Sitter space (the portion of it covered by the static patch).
Reissner-Nordström space
The Weyl solution, a static axisymmetric solution of the Einstein vacuum field equations 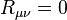$R_{{\mu \nu }}=0$ discovered by Hermann Weyl

External links

Concepts of General Relativity - A first principles demonstration of the metric in static spacetime

M. Sanchez, On the geometry of static space-times, preprint, 2004.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.