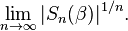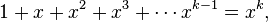Stanley–Wilf conjecture

From Wikipedia, the free encyclopedia

The Stanley–Wilf conjecture, formulated independently by Richard P. Stanley and Herbert Wilf in the late 1980s, states that every permutation pattern defines a set of permutations whose growth rate is singly exponential. It was proved by Adam Marcus and Gábor Tardos (2004) and is no longer a conjecture. Marcus and Tardos actually proved a different conjecture, due to Zoltán Füredi and Péter Hajnal (1992), which had been shown to imply the Stanley–Wilf conjecture by Klazar (2000).

Statement

The Stanley–Wilf conjecture states that for every permutation β, there is a constant C such that the number |S_n(β)| of permutations of length n which avoid β as a permutation pattern is at most Cⁿ. As Arratia (1999) observed, this is equivalent to the convergence of the limit

$\lim _{{n\to \infty }}|S_{n}(\beta )|^{{1/n}}.$

The upper bound given by Marcus and Tardos for C is exponential in the length of β. A stronger conjecture of Arratia (1999) had stated that one could take C to be (k − 1)², where k denotes the length of β, but this conjecture was disproved for the permutation β = 4231 by Albert et al. (2006). Indeed, Fox (preprint) has shown that C is, in fact, exponential in k for almost all permutations.

Allowable growth rates

Not every growth rate of the form Cⁿ may be achieved by a permutation class, regardless of whether it is defined by a single forbidden permutation pattern or a set of forbidden patterns. If the number of permutations in a permutation class grows at more than a polynomial rate, it must grow at least as quickly as the Fibonacci numbers. More specifically, define the growth constant (or Stanley–Wilf limit) of a permutation class P, with f_P(n) permutations of length n, to be

$\limsup _{{n\to \infty }}f_{P}(n)^{{1/n}}.$

If the growth constant is zero, then f_P(n) must be a polynomial. If it is not zero, then it must be the largest root of a polynomial of the form

$1+x+x^{2}+x^{3}+\cdots x^{{k-1}}=x^{k},$

for an integer k ≥ 2. For k = 2, C is the golden ratio, the base of the growth rate of the Fibonacci numbers. In general, as k grows larger, these roots approach 2. Thus, in this range, there are only a countably infinite number of growth rates possible.^[1] However, for every C > 2.48188 there exists a permutation class (possibly with infinitely many forbidden patterns) whose growth constant is C.^[2]

Notes

↑ Klazar (2010); Kaiser & Klazar (2003).
↑ Klazar (2010); Vatter (2010).

References

Albert, Michael H.; Elder, Murray; Rechnitzer, Andrew; Westcott, P.; Zabrocki, Mike (2006), "On the Stanley–Wilf limit of 4231-avoiding permutations and a conjecture of Arratia", Advances in Applied Mathematics 36 (2): 96–105, doi:10.1016/j.aam.2005.05.007, MR 2199982 .
Arratia, Richard (1999), "On the Stanley–Wilf conjecture for the number of permutations avoiding a given pattern", Electronic Journal of Combinatorics 6: N1, MR 1710623 .
Fox, Jacob (preprint), Stanley-Wilf limits are typically exponential, arXiv:1310.8378 Check date values in: |date= (help).
Füredi, Zoltán; Hajnal, Péter (1992), "Davenport–Schinzel theory of matrices", Discrete Mathematics 103 (3): 233–251, doi:10.1016/0012-365X(92)90316-8, MR 1171777 .
Kaiser, Tomáš; Klazar, Martin (March 2002), "On growth rates of closed permutation classes", Electronic Journal of Combinatorics 9 (2): Research paper 10, 20, MR 2028280 .
Klazar, Martin (2000), "The Füredi–Hajnal conjecture implies the Stanley–Wilf conjecture", Formal Power Series and Algebraic Combinatorics (Moscow, 2000), Springer, pp. 250–255, MR 1798218 .
Klazar, Martin (2010), "Some general results in combinatorial enumeration", Permutation patterns, London Math. Soc. Lecture Note Ser. 376, Cambridge: Cambridge Univ. Press, pp. 3–40, doi:10.1017/CBO9780511902499.002, MR 2732822 .
Marcus, Adam; Tardos, Gábor (2004), "Excluded permutation matrices and the Stanley–Wilf conjecture", Journal of Combinatorial Theory, Series A 107 (1): 153–160, doi:10.1016/j.jcta.2004.04.002, MR 2063960 .
Vatter, Vincent (2010), "Permutation classes of every growth rate above 2.48188", Mathematika 56 (1): 182–192, doi:10.1112/S0025579309000503, MR 2604993 .

External links

A Description of The Stanley–Wilf Conjecture – by Doron Zeilberger.
Weisstein, Eric W., "Stanley-Wilf conjecture", MathWorld.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.