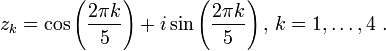Stable polynomial

From Wikipedia, the free encyclopedia

A polynomial is said to be stable if either:

  • all its roots lie in the open left half-plane, or
  • all its roots lie in the open unit disk.

The first condition provides stability for (or continuous-time) linear systems, and the second case relates to stability of discrete-time linear systems. A polynomial with the first property is called at times a Hurwitz polynomial and with the second property a Schur polynomial. Stable polynomials arise in control theory and in mathematical theory of differential and difference equations. A linear, time-invariant system (see LTI system theory) is said to be BIBO stable if every bounded input produces bounded output. A linear system is BIBO stable if its characteristic polynomial is stable. The denominator is required to be Hurwitz stable if the system is in continuous-time and Schur stable if it is in discrete-time. In practice, stability is determined by applying any one of several stability criteria.

Properties

  • The Routh-Hurwitz theorem provides an algorithm for determining if a given polynomial is Hurwitz stable.
  • To test if a given polynomial P (of degree d) is Schur stable, it suffices to apply this theorem to the transformed polynomial
Q(z)=(z-1)^{d}P\left({{z+1} \over {z-1}}\right)

obtained after the Möbius transformation z\mapsto {{z+1} \over {z-1}} which maps the left half-plane to the open unit disc: P is Schur stable if and only if Q is Hurwitz stable. For higher degree polynomials the extra computation involved in this mapping can be avoided by testing the Schur stability by the Schur-Cohn test, the Jury test or the Bistritz test.

  • Necessary condition: a Hurwitz stable polynomial (with real coefficients) has coefficients of the same sign (either all positive or all negative).
  • Sufficient condition: a polynomial f(z)=a_{0}+a_{1}z+\cdots +a_{n}z^{n} with (real) coefficients such that:
a_{n}>a_{{n-1}}>\cdots >a_{0}>0,

is Schur stable.

  • Product rule: Two polynomials f and g are stable (of the same type) if and only if the product fg is stable.

Examples

  • 4z^{3}+3z^{2}+2z+1 is Schur stable because it satisfies the sufficient condition;
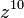  • z^{{10}} is Schur stable (because all its roots equal 0) but it does not satisfy the sufficient condition;
  • z^{2}-z-2 is not Hurwitz stable (its roots are -1,2) because it violates the necessary condition;
  • z^{2}+3z+2 is Hurwitz stable (its roots are -1,-2).
  • The polynomial z^{4}+z^{3}+z^{2}+z+1 (with positive coefficients) is neither Hurwitz stable nor Schur stable. Its roots are the four primitive fifth roots of unity
z_{k}=\cos \left({{2\pi k} \over 5}\right)+i\sin \left({{2\pi k} \over 5}\right),\,k=1,\ldots ,4\ .
Note here that
\cos({{2\pi }/5})={{{\sqrt {5}}-1} \over 4}>0.
It is a "boundary case" for Schur stability because its roots lie on the unit circle. The example also shows that the necessary (positivity) conditions stated above for Hurwitz stability are not sufficient.

See also

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.