Square One (puzzle)

From Wikipedia, the free encyclopedia

The Square One, also known as Back to Square One and Cube 21, is a puzzle similar to the Rubik's Cube. Its distinguishing feature among the numerous Rubik's Cube variants is that it can change shape as it is twisted, due to the way it is cut, thus adding an extra level of challenge and difficulty. The Super Square One and Square Two puzzles have been recently introduced. The Super Square One has two additional layers that can be scrambled and solved independently of the rest of the puzzle, and the Square Two has extra cuts made to the top and bottom layer, making the edge and corner wedges the same size.

The Square One puzzle in one of its unsolved states.
The same puzzle in its original (solved) state.

History

The Square One, with the full name "Back to Square One", and alternative name "Cube 21", was invented by Karel Hršel and Vojtěch Kopský around 1990. Application for Czechoslovak patent was filed on 8 November 1990, the patent was approved on 26 October 1992 with patent number CS 277266 B6. On March 16, 1993, it was patented in the USA with patent number US5,193,809. Its design was also patented on October 5, 1993, with patent number D340,093.

Description

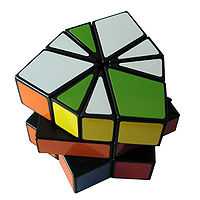
The Square One consists of three layers. The upper and lower layers contain kite and triangular pieces. They are also called corner and edge pieces, respectively. There are all together 8 kite and 8 triangular pieces. The kite pieces are 60 degrees wide, while the triangular pieces are 30 degrees wide, relative to the center of the layer.

The middle layer contains two trapezoid pieces, which together may form an irregular hexagon or a square.

Each layer can be rotated freely, and if the boundaries of pieces in all layers line up, the puzzle can be twisted vertically, interchanging half of the top layer with half of the bottom. In this way, the pieces of the puzzle can be scrambled. Note that because the kite pieces are precisely twice the angular width of the triangular pieces, the two can be freely intermixed, with two triangular pieces taking the place of a single kite piece and vice versa. This leads to bizarre shape changes within the puzzle at any point.

For the puzzle to be in cube shape, the upper and lower layers must have alternating kite and triangular pieces, with 4 kite and 4 triangular pieces on each layer, and the middle layer must have a square shape. However, since only two shapes are possible for the middle layer, there is a quick sequence of twists which changes the shape of the middle layer from one to the other without touching the rest of the puzzle.

Once the puzzle has a cube shape, the upper and lower layers are cut in an Iron Cross-like fashion, or equivalently cut by two concentric (standard) crosses, that make an angle with each other.

Like Rubik's Cube, the pieces are coloured. For the puzzle to be solved, not only does it need to be in cube shape, but each face of the cube must also have a uniform colour. In its solved (or original) state, viewing the cube from the face with the word "Square-1" printed on it, the colours are: white on top, green on the bottom, yellow in front, red on the left, orange on the right, and blue behind. Alternative versions of the Square One may have different colour schemes.

The Square One puzzle was sold in this shape with instructions for turning it back to a cube. This is halfway through a vertical turn.

Solutions

A good number of solutions for this puzzle exist on the Internet. Some solutions employ the classical layer-by-layer method, while other approaches include putting the corner pieces in place first, then the edge pieces, or vice versa. Some solutions are a combination of these approaches. Although these solutions use different approaches, most of them try to restore the cube shape of the puzzle first, regardless of the placement of the pieces and the parity of the middle layer, and then proceed to put the pieces in their correct places while preserving the cube shape.

The majority of solutions provide a large set of algorithms. These are sequences of turns and twists that will rearrange a small number of pieces while leaving the rest of the puzzle untouched. Examples include swapping two pieces, cycling through three pieces, etc. Larger scale algorithms are also possible, such as interchanging the top and bottom layers. Through the systematic use of these algorithms, the puzzle is gradually solved.

Like solutions of the Rubik's Cube, the solutions of Square One depend on the use of algorithms discovered either by trial and error, or by using computer searches. However, while solutions of Rubik's Cube rely on these algorithms more towards the end, they are heavily used throughout the course of solving the Square One. This is because the uniform shape of the pieces in the Rubik's Cube allows one to focus on positioning a small subset of pieces while disregarding the rest, at least at the beginning of a solution. However, with the Square One, the free intermixing of corner and edge pieces can sometimes cause a certain desired operation to be physically blocked; so one must take all pieces into account right from the beginning. Some solutions of the Square One rely solely on the use of algorithms.

Number of positions

If different rotations of a given permutation are counted only once while reflections are counted individually, there are 170 × 2 × 8! × 8! = 552,738,816,000 positions.

If both rotations and reflections are counted once only, the number of positions reduces to 15! ÷ 3 = 435,891,456,000. Also, it always can be solved in a maximum of 14 moves.

Records

Bingliang Li of China holds the world record single (8.65 seconds, set at the Guangdong Open 2010) and average (11.31 seconds, set at Guiyang Open 2012) for the Square-1.[1]

Super Square One

The Super Square One, scrambled
The Super Square One, solved
The Super Square One, in one of its many possible shapes

The Super Square One is a 4-layer version of the Square One. Just like the Square One, it can adopt non-cubic shapes as it is twisted. As of 2009, it is sold by Uwe Mèffert in his puzzle shop, Meffert's.

It consists of 4 layers of 8 pieces, each surrounding a circular column which can be rotated along a perpendicular axis. This allows the pieces from the top and bottom layers and the middle two layers to be interchanged. Each layer consists of 8 movable pieces: 4 wider wedges and 4 narrower wedges. In the top and bottom layers, the wider pieces are the "corner" pieces, and the narrower pieces are the "edge pieces". In the middle two layers, the wider pieces are the "edge" pieces, and the narrower pieces are the "face centers". The wider pieces are exactly twice the angular width of the narrower pieces, so that two narrower pieces can fit in the place of one wider piece. Thus, they can be freely intermixed. This leads to the puzzle adopting a large variety of non-cubic shapes.

Solution

Despite its appearance, the Super Square One is not significantly more difficult to solve than the original Square One. The middle layers are nearly identical to the top and bottom layers of the Square One, and may be solved independently using the same methods as the Square One. The corners of the middle layers are distinguishable because the corners with the same two colors are mirror images of each other, but the middle edges of each face are interchangeable since they show only one color each.

Number of positions

Square Two

The "Square Two" is yet another variation of the popular Square One puzzle, with extra cuts on the top and bottom layers. It is also currently marketed by Meffert's online store.

The Square Two is mechanically the same as a Square One, but the large corner wedges of the top and bottom layers are cut in half, effectively making the corner wedges as versatile as the edge wedges. This removes the locking issue present on the Square One, which in many ways makes the Square Two easier to solve (and scramble) than its predecessor.

Solution

The Square Two, like the Super Square One, isn't much more difficult than the Square One. In many ways, it's actually easier considering one can always make a slice turn regardless of the positions of the top and bottom layers. Mostly, it's solved just like the Original, merely requiring the extra step of combining the corner wedges. After that, it is solved exactly like the Square One.

Number of positions

There are a total of 24 wedge pieces on the puzzle.

Any permutation of the wedge pieces is possible, including even and odd permutations. This implies there are 24!=620,448,401,733,239,439,360,000 possible permutations of these pieces.

However, the middle layer has two possible orientations for each position, increasing the number of positions by a factor of 2.

This would theoretically yield a grand total of (24!)*2=1,240,896,803,466,478,878,720,000 possible positions for the puzzle, but since the layers have 12 different orientations for each position, some positions have been counted too many times this way. This reduces the number of positions by 12^2.

The final count is (24!)/72=8,617,338,912,961,658,880,000 total possible positions.

See also

References

  1. ↑ "Official Records of WCA". worldcubeassociation.org. 

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.