Square-lattice Ising model
In statistical mechanics, the two-dimensional square-lattice Ising model is a simple model of interacting magnetic spins. The model is notable for having nontrivial interactions, yet having an analytical solution. The model was solved by (Lars Onsager 1944) for the special case that the external magnetic field H = 0. An analytical solution for the general case for  has yet to be found.
has yet to be found.
Definition of the model
Consider the 2D Ising model on a square lattice  with N sites, with periodic boundary conditions in both the horizontal and vertical directions, which effectively reduces the geometry of the model to a torus. In a general case, the horizontal coupling J is not equal to the coupling in the vertical direction, J*. With an equal number of rows and columns in the lattice, there will be N of each. In terms of
with N sites, with periodic boundary conditions in both the horizontal and vertical directions, which effectively reduces the geometry of the model to a torus. In a general case, the horizontal coupling J is not equal to the coupling in the vertical direction, J*. With an equal number of rows and columns in the lattice, there will be N of each. In terms of
where  where T is absolute temperature and k is Boltzmann's constant, the partition function
where T is absolute temperature and k is Boltzmann's constant, the partition function 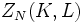 is given by
is given by
Critical temperature
The critical temperature  can be obtained from the Kramers–Wannier duality relation. Denoting the free energy per site as
can be obtained from the Kramers–Wannier duality relation. Denoting the free energy per site as  , one has:
, one has:
where
Assuming there is only one critical line in the (K,L) plane, the duality relation implies that this is given by:
For the isotropic case  , one finds the famous relation for the critical temperature
, one finds the famous relation for the critical temperature 
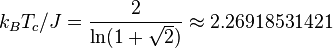 .
.
Dual lattice
Consider a configuration of spins 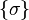 on the square lattice
on the square lattice  . Let r and s denote the number of unlike neighbours in the vertical and horizontal directions respectively. Then the summand in
. Let r and s denote the number of unlike neighbours in the vertical and horizontal directions respectively. Then the summand in  corresponding to
corresponding to 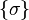 is given by
is given by

Construct a dual lattice  as depicted in the diagram. For every configuration
as depicted in the diagram. For every configuration 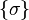 , a polygon is associated to the lattice by drawing a line on the edge of the dual lattice if the spins separated by the edge are unlike. Since by traversing a vertex of
, a polygon is associated to the lattice by drawing a line on the edge of the dual lattice if the spins separated by the edge are unlike. Since by traversing a vertex of  the spins need to change an even number of times so that one arrives at the starting point with the same charge, every vertex of the dual lattice is connected to an even number of lines in the configuration, defining a polygon.
the spins need to change an even number of times so that one arrives at the starting point with the same charge, every vertex of the dual lattice is connected to an even number of lines in the configuration, defining a polygon.
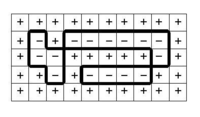
This reduces the partition function to
summing over all polygons in the dual lattice, where r and s are the number of horizontal and vertical lines in the polygon, with the factor of 2 arising from the inversion of spin configuration.
Low-temperature expansion
At low temperatures, K, L approach infinity, so that as 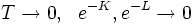 , so that
, so that
defines a low temperature expansion of 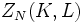 .
.
High-temperature expansion
Since  one has
one has
Therefore
where  and
and  . Since there are N horizontal and vertical edges, there are a total of
. Since there are N horizontal and vertical edges, there are a total of 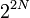 terms in the expansion. Every term corresponds to a configuration of lines of the lattice, by associating a line connecting i and j if the term
terms in the expansion. Every term corresponds to a configuration of lines of the lattice, by associating a line connecting i and j if the term  (or
(or  is chosen in the product. Summing over the configurations, using
is chosen in the product. Summing over the configurations, using
shows that only configurations with an even number of lines at each vertex (polygons) will contribute to the partition function, giving
where the sum is over all polygons in the lattice. Since tanh K, tanh L 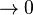 as
as 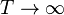 , this gives the high temperature expansion of
, this gives the high temperature expansion of 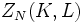 .
.
The two expansions can be related using the Kramers-Wannier duality.
Exact solution
The free energy per site in the limit  is given as follows. Define the parameter k as:
is given as follows. Define the parameter k as:
The free energy per site F can be expressed as:
For the isotropic case  , from the above expression one finds for the internal energy per site:
, from the above expression one finds for the internal energy per site:
and the spontaneous magnetization is, for  :
:
References
- Baxter, Rodney J. (1982), Exactly solved models in statistical mechanics, London: Academic Press Inc. [Harcourt Brace Jovanovich Publishers], ISBN 978-0-12-083180-7, MR 690578
- K. Binder (2001), "Ising model", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Stephen G. Brush (1967), History of the Lenz-Ising Model. Reviews of Modern Physics (American Physical Society) vol. 39, pp 883–893. doi:10.1103/RevModPhys.39.883
- Huang, Kerson (1987), Statistical mechanics (2nd edition), Wiley, ISBN 0471815187
- Ising, E. (1925), "Beitrag zur Theorie des Ferromagnetismus", Z. Phys. 31: 253–258, Bibcode:1925ZPhy...31..253I, doi:10.1007/BF02980577
- Itzykson, Claude; Drouffe, Jean-Michel (1989), Théorie statistique des champs, Volume 1, Savoirs actuels (CNRS), EDP Sciences Editions, ISBN 2868833608
- Itzykson, Claude; Drouffe, Jean-Michel (1989), Statistical field theory, Volume 1: From Brownian motion to renormalization and lattice gauge theory, Cambridge University Press, ISBN 0521408059
- Barry M. McCoy and Tai Tsun Wu (1973), The Two-Dimensional Ising Model. Harvard University Press, Cambridge Massachusetts, ISBN 0-674-91440-6
- Montroll, Elliott W.; Potts, Renfrey B.; Ward, John C. (1963), "Correlations and spontaneous magnetization of the two-dimensional Ising model", Journal of Mathematical Physics 4: 308–322, Bibcode:1963JMP.....4..308M, doi:10.1063/1.1703955, ISSN 0022-2488, MR 0148406
- Onsager, Lars (1944), "Crystal statistics. I. A two-dimensional model with an order-disorder transition", Phys. Rev., Series II 65: 117–149, Bibcode:1944PhRv...65..117O, doi:10.1103/PhysRev.65.117, MR 0010315
- Onsager, Lars (1949), "Discussion", Nuovo Cimento (suppl.) 6: 261
- John Palmer (2007), Planar Ising Correlations. Birkhäuser, Boston, ISBN 978-0-8176-4248-8.
- Yang, C. N. (1952), "The spontaneous magnetization of a two-dimensional Ising model", Physical Review, Series II 85: 808–816, Bibcode:1952PhRv...85..808Y, doi:10.1103/PhysRev.85.808, MR 0051740

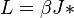

![\beta F\left(K^{{*}},L^{{*}}\right)=\beta F\left(K,L\right)+{\frac {1}{2}}\log \left[\sinh \left(2K\right)\sinh \left(2L\right)\right]](/2014-wikipedia_en_all_02_2014/I/media/a/e/7/3/ae7349e2392e7def251f89578f563c22.png)


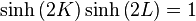

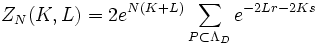
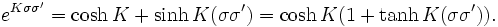

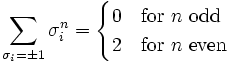
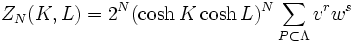

![-\beta F={\frac {\log(2)}{2}}+{\frac {1}{2\pi }}\int _{{0}}^{{\pi }}\log \left[\cosh \left(2K\right)\cosh \left(2L\right)+{\frac {1}{k}}{\sqrt {1+k^{{2}}-2k\cos(2\theta )}}\right]d\theta](/2014-wikipedia_en_all_02_2014/I/media/0/f/1/8/0f18d2e442b877bde6c85029caa1444d.png)
![U=-J\coth(2\beta J)\left[1+{\frac {2}{\pi }}(2\tanh ^{2}(2\beta J)-1)\int _{0}^{{\pi /2}}{\frac {1}{{\sqrt {1-4k(1+k)^{{-2}}\sin ^{2}(\theta )}}}}d\theta \right]](/2014-wikipedia_en_all_02_2014/I/media/f/8/1/c/f81c22f88a988187dcedf35222cb9964.png)
![M=\left[1-\sinh ^{{-4}}(2\beta J)\right]^{{1/8}}](/2014-wikipedia_en_all_02_2014/I/media/1/b/4/0/1b409597bb98fd234100e335d3aec3b9.png)