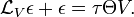Spray (mathematics)
In differential geometry, a spray is a vector field H on the tangent bundle TM that encodes a quasilinear second order system of ordinary differential equations on the base manifold M. Usually a spray is required to be homogeneous in the sense that its integral curves t→ΦHt(ξ)∈TM obey the rule ΦHt(λξ)=ΦHλt(ξ) in positive reparameterizations. If this requirement is dropped, H is called a semispray.
Sprays arise naturally in Riemannian and Finsler geometry as the geodesic sprays, whose integral curves are precisely the tangent curves of locally length minimizing curves. Semisprays arise naturally as the extremal curves of action integrals in Lagrangian mechanics. Generalizing all these examples, any (possibly nonlinear) connection on M induces a semispray H, and conversely, any semispray H induces a torsion-free nonlinear connection on M. If the original connection is torsion-free it coincides with the connection induced by H, and homogeneous torsion-free connections are in one-to-one correspondence with full sprays.[1]
Formal definitions
Let M be a differentiable manifold and (TM,πTM,M) its tangent bundle. Then a vector field H on TM (that is, a section of the double tangent bundle TTM) is a semispray on M, if any of the three following equivalent conditions holds:
- (πTM)*Hξ = ξ.
- JH=V, where J is the tangent structure on TM and V is the canonical vector field on TM\0.
- j∘H=H, where j:TTM→TTM is the canonical flip and H is seen as a mapping TM→TTM.
A semispray H on M is a (full) spray if any of the following equivalent conditions hold:
- Hλξ = λ*(λHξ), where λ*:TTM→TTM is the push-forward of the multiplication λ:TM→TM by a positive scalar λ>0.
- The Lie-derivative of H along the canonical vector field V satisfies [V,H]=H.
- The integral curves t→ΦHt(ξ)∈TM\0 of H satisfy ΦHt(λξ)=ΦHλt(ξ) for any λ>0.
Let (xi,ξi) be the local coordinates on TM associated with the local coordinates (xi) on M using the coordinate basis on each tangent space. Then H is a semispray on M if and only if it has a local representation of the form
on each associated coordinate system on TM. The semispray H is a (full) spray, if and only if the spray coefficients Gi satisfy
Semisprays in Lagrangian mechanics
A physical system is modeled in Lagrangian mechanics by a Lagrangian function L:TM→R on the tangent bundle of some configuration space M. The dynamical law is obtained from the Hamiltonian principle, which states that the time evolution γ:[a,b]→M of the state of the system is stationary for the action integral
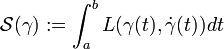 .
.
In the associated coordinates on TM the first variation of the action integral reads as
where X:[a,b]→R is the variation vector field associated with the variation γs:[a,b]→M around γ(t) = γ0(t). This first variation formula can be recast in a more informative form by introducing the following concepts:
- The covector
 with
with  is the conjugate momentum of
is the conjugate momentum of  .
. - The corresponding one-form
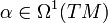 with
with  is the Hilbert-form associated with the Lagrangian.
is the Hilbert-form associated with the Lagrangian. - The bilinear form
 with
with  is the fundamental tensor of the Lagrangian at
is the fundamental tensor of the Lagrangian at  .
. - The Lagrangian satisfies the Legendre condition if the fundamental tensor
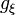 is non-degenerate at every
is non-degenerate at every  . Then the inverse matrix of
. Then the inverse matrix of  is denoted by
is denoted by  .
. - The Energy associated with the Lagrangian is
 .
.
If the Legendre condition is satisfied, then dα∈Ω2(TM) is a symplectic form, and there exists a unique Hamiltonian vector field H on TM corresponding to the Hamiltonian function E such that
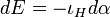 .
.
Let (Xi,Yi) be the components of the Hamiltonian vector field H in the associated coordinates on TM. Then
and
so we see that the Hamiltonian vector field H is a semispray on the configuration space M with the spray coefficients
Now the first variational formula can be rewritten as
and we see γ[a,b]→M is stationary for the action integral with fixed end points if and only if its tangent curve γ':[a,b]→TM is an integral curve for the Hamiltonian vector field H. Hence the dynamics of mechanical systems are described by semisprays arising from action integrals.
Geodesic spray
The locally length minimizing curves of Riemannian and Finsler manifolds are called geodesics. Using the framework of Lagrangian mechanics one can describe these curves with spray structures. Define a Lagrangian function on TM by
where F:TM→R is the Finsler function. In the Riemannian case one uses F2(x,ξ) = gij(x)ξiξj. Now introduce the concepts from the section above. In the Riemannian case it turns out that the fundamental tensor gij(x,ξ) is simply the Riemannian metric gij(x). In the general case the homogeneity condition
of the Finsler-function implies the following formulae:
In terms of classical mechanical the last equation states that all the energy in the system (M,L) is in the kinetic form. Furthermore, one obtains the homogeneity properties
of which the last one says that the Hamiltonian vector field H for this mechanical system is a full spray. The constant speed geodesics of the underlying Finsler (or Riemannian) manifold are described by this spray for the following reasons:
- Since gξ is positive definite for Finsler spaces, every short enough stationary curve for the length functional is length minimizing.
- Every stationary curve for the action integral is of constant speed
 , since the energy is automatically a constant of motion.
, since the energy is automatically a constant of motion. - For any curve
![\gamma :[a,b]\to M](/2014-wikipedia_en_all_02_2014/I/media/7/f/a/b/7fab592a63121a749a125e0b9a639a0c.png) of constant speed the action integral and the length functional are related by
of constant speed the action integral and the length functional are related by
Therefore a curve ![\gamma :[a,b]\to M](/2014-wikipedia_en_all_02_2014/I/media/7/f/a/b/7fab592a63121a749a125e0b9a639a0c.png) is stationary to the action integral if and only if it is of constant speed and stationary to the length functional. The Hamiltonian vector field H is called the geodesic spray of the Finsler manifold (M,F) and the corresponding flow ΦHt(ξ) is called the geodesic flow.
is stationary to the action integral if and only if it is of constant speed and stationary to the length functional. The Hamiltonian vector field H is called the geodesic spray of the Finsler manifold (M,F) and the corresponding flow ΦHt(ξ) is called the geodesic flow.
Correspondence with nonlinear connections
A semispray H on a smooth manifold M defines an Ehresmann-connection T(TM\0) = H(TM\0) ⊕ V(TM\0) on the slit tangent bundle through its horizontal and vertical projections
This connection on TM\0 always has a vanishing torsion tensor, which is defined as the Frölicher-Nijenhuis bracket T=[J,v]. In more elementary terms the torsion can be defined as
Introducing the canonical vector field V on TM\0 and the adjoint structure Θ of the induced connection the horizontal part of the semispray can be written as hH=ΘV. The vertical part ε=vH of the semispray is known as the first spray invariant, and the semispray H itself decomposes into
The first spray invariant is related to the tension
of the induced non-linear connection through the ordinary differential equation
Therefore the first spray invariant ε (and hence the whole semi-spray H) can be recovered from the non-linear connection by
From this relation one also sees that the induced connection is homogeneous if and only if H is a full spray.
Jacobi-fields of sprays and semisprays
A good source for Jacobi fields of semisprays is Section 4.4, Jacobi equations of a semispray, of the publicly available book Finsler-Lagrange Geometry by Bucutaru and Miron. Of particular note is their concept of a dynamical covariant derivative. In another paper by Bucutaru, Constantinescu and Dahl relate this concept to that of the Kosambi biderivative operator.
For a good introduction to Kosambi's methods, see the article, What is Kosambi-Cartan-Chern theory?.
References
- ↑ I.Bucataru, R.Miron, Finsler-Lagrange Geometry, Editura Academiei Române, 2007.
- Sternberg, Shlomo (1964), Lectures on Differential Geometry, Prentice-Hall.
- Lang, Serge (1999), Fundamentals of Differential Geometry, Springer-Verlag.
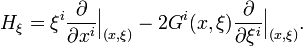
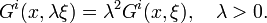

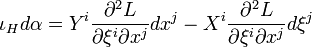

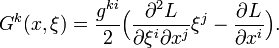
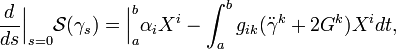

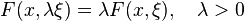
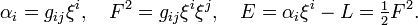
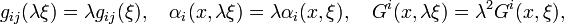
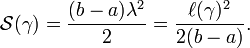

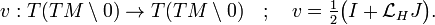
![\displaystyle T(X,Y)=J[hX,hY]-v[JX,hY)-v[hX,JY].](/2014-wikipedia_en_all_02_2014/I/media/1/e/0/f/1e0f934162536b811ea9e748f3e70758.png)
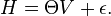
![\tau ={\mathcal L}_{V}v={\tfrac {1}{2}}{\mathcal L}_{{[V,H]-H}}J](/2014-wikipedia_en_all_02_2014/I/media/3/b/5/c/3b5cb0ae94ebeaace237d39b41960bd7.png)