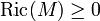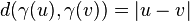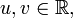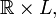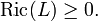Splitting theorem
From Wikipedia, the free encyclopedia
The splitting theorem is a classical theorem in Riemannian geometry. It states that if a complete Riemannian manifold M with Ricci curvature
has a straight line, i.e., a geodesic γ such that
for all
then it is isometric to a product space
where 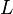 is a Riemannian manifold with
is a Riemannian manifold with
History
For the surfaces, the theorem was proved by Stephan Cohn-Vossen.[1] Victor Andreevich Toponogov generalized it to manifolds with non-negative sectional curvature. [2] Jeff Cheeger and Detlef Gromoll proved that non-negative Ricci curvature is sufficient.
Later the splitting theorem was extended to Lorentzian manifolds with nonnegative Ricci curvature in the time-like directions.[3] [4] [5]
References
- ↑ S. Cohn-Vossen, “Totalkrümmung und geodätische Linien auf einfachzusammenhängenden offenen vollständigen Flächenstücken”, Матем. сб., 1(43):2 (1936), 139–164
- ↑ Toponogov, V. A. Riemannian spaces containing straight lines. (Russian) Dokl. Akad. Nauk SSSR 127 1959 977–979.
- ↑ Eschenburg, J.-H. The splitting theorem for space-times with strong energy condition. J. Differential Geom. 27 (1988), no. 3, 477–491.
- ↑ Galloway, Gregory J.(1-MIAM) The Lorentzian splitting theorem without the completeness assumption. J. Differential Geom. 29 (1989), no. 2, 373–387.
- ↑ Newman, Richard P. A. C. A proof of the splitting conjecture of S.-T. Yau. J. Differential Geom. 31 (1990), no. 1, 163–184.
- Jeff Cheeger; Detlef Gromoll, The splitting theorem for manifolds of nonnegative Ricci curvature, Journal of Differential Geometry 6 (1971/72), 119–128. MR 0303460
- V. A. Toponogov, Riemann spaces with curvature bounded below (Russian), Uspehi Mat. Nauk 14 (1959), no. 1 (85), 87–130. MR 0103510
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.