Splitting principle

From Wikipedia, the free encyclopedia

In mathematics, the splitting principle is a technique used to reduce questions about vector bundles to the case of line bundles.

In the theory of vector bundles, one often wishes to simplify computations, say of Chern classes. Often computations are well understood for line bundles and for direct sums of line bundles. In this case the splitting principle can be quite useful.

Theorem: Splitting Principle: Let 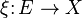$\xi \colon E\rightarrow X$ be a vector bundle of rank $n$ over a manifold $X$ . There exists a space $Y=Fl(E)$ , called the flag bundle associated to $E$ , and a map $p\colon Y\rightarrow X$ such that

the induced cohomology homomorphism 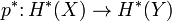$p^{*}\colon H^{*}(X)\rightarrow H^{*}(Y)$ is injective, and
the pullback bundle $p^{*}\xi \colon p^{*}E\rightarrow Y$ breaks up as a direct sum of line bundles: $p^{*}(E)=L_{1}\oplus L_{2}\oplus \cdots \oplus L_{n}.$

The line bundles $L_{i}$ or their first characteristic class are called Chern roots.

The fact that 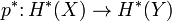$p^{*}\colon H^{*}(X)\rightarrow H^{*}(Y)$ is injective means that any equation which holds in $H^{*}(Y)$ (say between various Chern classes) also holds in $H^{*}(X)$ .

The point is that these equations are easier to understand for direct sums of line bundles than for arbitrary vector bundles, so equations should be understood in $Y$ and then pushed down to $X$ .

Symmetric polynomial

Under the splitting principle, characteristic classes correspond to symmetric polynomials (and for the Euler class, alternating polynomials) in the class of line bundles.

The Chern classes and Pontryagin classes correspond to symmetric polynomials: they are symmetric polynomials in the corresponding classes of line bundles ( $p_{k}$ is the kth symmetric polynomial in the $p_{1}$ of the line bundles, and so forth).

The Euler class is an invariant of an oriented vector bundle, and thus the line bundles are ordered up to sign; the corresponding polynomial is the Vandermonde polynomial, the basic alternating polynomial. Further, for an even dimensional manifold, its square is the top Pontryagin class, which corresponds to the square of the Vandermonde polynomial being the discriminant.

References

Hatcher, Allen (2003), Vector Bundles & K-Theory (2.0 ed.) section 3.1
Bott and Tu. Differential Forms in Algebraic Topology, section 21.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Splitting principle

Symmetric polynomial

See also

References