Spinel group

From Wikipedia, the free encyclopedia

The spinels are any of a class of minerals of general formulation A2+B23+O42- which crystallise in the cubic (isometric) crystal system, with the oxide anions arranged in a cubic close-packed lattice and the cations A and B occupying some or all of the octahedral and tetrahedral sites in the lattice. A and B can be divalent, trivalent, or quadrivalent cations, including magnesium, zinc, iron, manganese, aluminium, chromium, titanium, and silicon. Although the anion is normally oxide, the analogous thiospinel structure includes the rest of the chalcogenides. A and B can also be the same metal under different charges, such as the case in Magnetite, Fe3O4 (as Fe2+Fe23+O42-), which is the most important member of the Spinel group.[1]

Members of the spinel group include:[2]

There are many more compounds with a spinel structure, e.g. the thiospinels and selenospinels, that can either be synthesized in the lab or in some cases occur as minerals.

The heterogenaity of spinel group members varies based on composition with Ferrous and magnesium based members varying greatly as in solid solution, which requires similarly sized cations. However Ferric and Aluminium based spinels are specimens are almost entirely homogeneous due to their large size difference. [3]

The spinel structure

Crystal structure of spinel

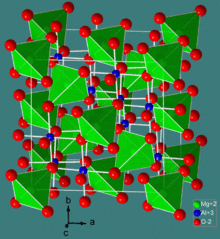
Normal spinel structures are usually cubic close-packed oxides with one octahedral and two tetrahedral sites per oxide. The tetrahedral points are smaller than the octahedral points. B3+ ions occupy the octahedral holes because of a charge factor, but can only occupy half of the octahedral holes. A2+ ions occupy 1/8 of the tetrahedral holes. A common example of a normal spinel is MgAl2O4.

Inverse spinel structures however are different in the cation distribution, in that all of the A cations and half of the B cations occupy octahedral sites, while the other half of the B cations occupy tetrahedral sites. A common example of an inverse spinel is Fe3O4, if the Fe2+ (A2+) ions are d6 high-spin and the Fe3+ (B3+) ions are d5 high-spin.

In addition, there are intermediate cases where the cation distribution can be described as (A1-xBx)[Ax/2B1-x/2]2O4, where parentheses () and brackets [] are used to denote tetrahedral and octahedral sites, respectively. The so-called inversion degree x adopts values between 0 (normal) and 1 (inverse), and it is x=2/3 for a fully random cation distribution.

In order to explain the adoption of a particular cation distribution in a spinel structure, one must take into account the crystal field stabilization energies (CFSE) of the transition metals present. Some ions may have a distinct preference on the octahedral site which is dependent on the d-electron count. If the A2+ ions have a strong preference for the octahedral site, they will force their way into it and displace half of the B3+ ions from the octahedral sites to the tetrahedral sites. If the B3+ ions have a low or zero octahedral site stabilization energy (OSSE), then they have no preference and will adopt the tetrahedral site.

Burdett and co-workers proposed an alternative treatment of the problem of spinel inversion, using the relative sizes of the s and p atomic orbitals of the two types of atom to determine their site preference.[4] This is because the dominant stabilizing interaction in the solids is not the crystal field stabilization energy generated by the interaction of the ligands with the d-electrons, but the σ-type interactions between the metal cations and the oxide anions. This rationale can explain anomalies in the spinel structures that crystal-field theory cannot, such as the marked preference of Al3+ cations for octahedral sites or of Zn2+ for tetrahedral sites - using crystal field theory would predict that both have no site preference. Only in cases where this size-based approach indicates no preference for one structure over another do crystal field effects make any difference — in effect they are just a small perturbation that can sometimes make a difference, but which often do not.

References

  1. ↑ Ernst, W. G. Earth Materials. Englewood Cliffs, NJ: Prentice-Hall, 1969. Print. p.58
  2. ↑ Spinel group at Mindat
  3. ↑ Ernst, W. G. Earth Materials. Englewood Cliffs, NJ: Prentice-Hall, 1969. Print. p.59
  4. ↑ J.K. Burdett, G.L. Price and S.L. Price (1982). "Role of the crystal-field theory in determining the structures of spinels". J. Am. Chem. Soc. 104: 92–95. doi:10.1021/ja00365a019. 
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.