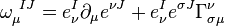Spin connection

From Wikipedia, the free encyclopedia

In differential geometry and mathematical physics, a spin connection is a connection on a spinor bundle. It is induced, in a canonical manner, from the affine connection. It can also be regarded as the gauge field generated by local Lorentz transformations. In some canonical formulations of general relativity, a spin connection is defined on spatial slices and can also be regarded as the gauge field generated by local rotations.

Definition

Let us first introduce the local Lorentz frame fields or vierbein (also known as a tetrad) 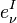e_{\nu }^{I}, this is basically four orthogonal space time vector fields labeled by 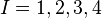I=1,2,3,4. Orthogonal meaning

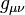g^{{\mu \nu }}e_{\mu }^{I}e_{\nu }^{J}=\eta ^{{IJ}}

where g^{{\mu \nu }} is the inverse matrix of g_{{\mu \nu }} is the spacetime metric and 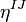\eta ^{{IJ}} is the Minkowski metric. Here, capital letters denote the local Lorentz frame indices; Greek indices denote general coordinate indices. The spacetime metric can be expressed by

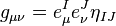
g_{{\mu \nu }}=e_{\mu }^{I}e_{\nu }^{J}\eta _{{IJ}}

which simply expresses that 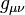g_{{\mu \nu }}, when written in terms of the basis 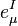e_{\mu }^{I}, is locally flat.

The spin connection 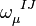\omega _{{\mu }}^{{\ IJ}} defines a covariant derivative 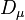D_{\mu } on generalized tensors. For example its action on V_{\nu }^{I} is

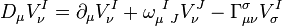
D_{\mu }V_{\nu }^{I}=\partial _{\mu }V_{\nu }^{I}+\omega _{{\mu \ J}}^{{\ I}}V_{\nu }^{J}-\Gamma _{{\mu \nu }}^{\sigma }V_{\sigma }^{I}

where \Gamma _{{\sigma \mu }}^{\nu } is the affine connection. The connection is said to be compatible to the vierbein if it satisfies

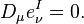
D_{\mu }e_{\nu }^{I}=0.

The spin connection 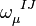\omega _{{\mu }}^{{\ IJ}} is then given by:

\omega _{{\mu }}^{{\ IJ}}=e_{\nu }^{I}\partial _{\mu }e^{{\nu J}}+e_{\nu }^{I}e^{{\sigma J}}\Gamma _{{\sigma \mu }}^{\nu }

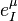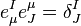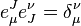where we have introduced the dual-vierbein e_{I}^{\mu } satisfying e_{\mu }^{I}e_{J}^{\mu }=\delta _{J}^{I} and e_{\mu }^{J}e_{J}^{\nu }=\delta _{\mu }^{\nu }. We expect that 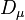D_{\mu } will also annihilate the Minkowski metric \eta _{{IJ}},

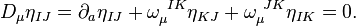
D_{\mu }\eta _{{IJ}}=\partial _{a}\eta _{{IJ}}+\omega _{{\mu }}^{{\ IK}}\eta _{{KJ}}+\omega _{{\mu }}^{{\ JK}}\eta _{{IK}}=0.

This implies that the connection is anti-symmetric in its internal indices, 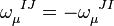\omega _{{\mu }}^{{\ IJ}}=-\omega _{{\mu }}^{{\ JI}}.

By substituting the formula for the affine connection 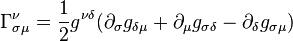\Gamma _{{\sigma \mu }}^{\nu }={1 \over 2}g^{{\nu \delta }}(\partial _{\sigma }g_{{\delta \mu }}+\partial _{\mu }g_{{\sigma \delta }}-\partial _{\delta }g_{{\sigma \mu }}) written in terms of the 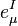e_{\mu }^{I}, the spin connection can be written entirely in terms of the e_{\mu }^{I},

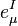\omega _{{\mu }}^{{\ IJ}}={1 \over 2}e^{{\nu [I}}(e_{{\mu ,\nu }}^{{J]}}-e_{{\nu ,\mu }}^{{J]}}+e^{{J]\sigma }}e_{\mu }^{K}e_{{\nu ,\sigma K}}).

To directly solve the compatibility condition for the spin connection 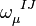\omega _{{\mu }}^{{\ IJ}}, one can use the same trick that was used to solve \nabla _{\rho }g_{{\alpha \beta }}=0 for the affine connection \Gamma _{{\alpha \beta }}^{\gamma }. First contract the compatibility condition to give

e_{J}^{\alpha }e_{K}^{\beta }(\partial _{{[\alpha }}e_{{\beta ]I}}+\omega _{{[\alpha I}}^{{\;\;\;\;L}}e_{{\beta ]L}})=0.

Then, do a cyclic permutation of the free indices 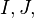I,J, and K, and add and subtract the three resulting equations:

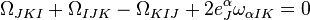
\Omega _{{JKI}}+\Omega _{{IJK}}-\Omega _{{KIJ}}+2e_{J}^{\alpha }\omega _{{\alpha IK}}=0

where we have used the definition \Omega _{{JKI}}:=e_{J}^{\alpha }e_{K}^{\beta }\partial _{{[\alpha }}e_{{\beta ]I}}. The solution for the spin connection is

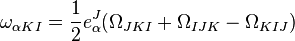\omega _{{\alpha KI}}={1 \over 2}e_{\alpha }^{J}(\Omega _{{JKI}}+\Omega _{{IJK}}-\Omega _{{KIJ}}).

From this we obtain the same formula as before.

Applications

The spin connection arises in the Dirac equation when expressed in the language of curved spacetime. Specifically there are problems coupling gravity to spinor fields: there are no finite dimensional spinor representations of the general covariance group. However, there are of course spinorial representations of the Lorentz group. This fact is utilized by employing tetrad fields describing a flat tangent space at every point of spacetime. The Dirac matrices 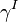\gamma ^{I} are contracted onto vierbiens,

\gamma ^{I}e_{I}^{\mu }(x)=\gamma ^{\mu }(x).

We wish to construct a generally covariant Dirac equation. Under a flat tangent space Lorentz transformation transforms the spinor as

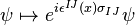
\psi \mapsto e^{{i\epsilon ^{{IJ}}(x)\sigma _{{IJ}}}}\psi

We have introduced local Lorentz transformatins on flat tangent space, so 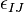\epsilon _{{IJ}} is a function of space-time. This means that the partial derivative of a spinor is no longer a genuine tensor. As usual, one introduces a connection field 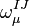\omega _{\mu }^{{IJ}} that allows us to gauge the Lorentz group. The covariant derivative defined with the spin connection is,

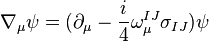\nabla _{\mu }\psi =(\partial _{\mu }-{i \over 4}\omega _{\mu }^{{IJ}}\sigma _{{IJ}})\psi ,

and is a genuine tensor and Dirac's equation is rewritten as

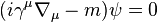(i\gamma ^{\mu }\nabla _{\mu }-m)\psi =0.

The generally covariant fermion action couples fermions to gravity when added to the first order tetradic Palatini action,

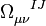{\mathcal {L}}=-{1 \over 2\kappa ^{2}}ee_{I}^{\mu }e_{J}^{\nu }\Omega _{{\mu \nu }}^{{\;\;\;\;IJ}}[\omega ]+e\overline {\psi }(i\gamma ^{\mu }\nabla _{\mu }-m)\psi

where e:=\det e_{\mu }^{I} and \Omega _{{\mu \nu }}^{{\;\;\;\;IJ}} is the curvature of the spin connection.

The tetradic Palatini formulation of general relativity which is a first order formulation of the Einstein-Hilbert action where the tetrad and the spin connection are the basic independent variables. In the 3+1 version of Palatini formulation, the information about the spatial metric, 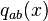q_{{ab}}(x), is encoded in the triad e_{a}^{i} (three dimensional, spatial version of the tetrad). 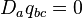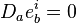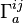Here we extend the metric compatibility condition D_{a}q_{{bc}}=0 to e_{a}^{i}, that is, D_{a}e_{b}^{i}=0 and we obtain a formula similar to the one given above but for the spatial spin connection \Gamma _{a}^{{ij}}.

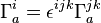The spatial spin connection appears in the definition of Ashtekar-Barbero variables which allows 3+1 general relativity to be rewritten as a special type of SU(2) Yang-Mills gauge theory. One defines \Gamma _{a}^{i}=\epsilon ^{{ijk}}\Gamma _{a}^{{jk}}. 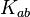The Ashtekar-Barbero connection variable is then defined as A_{a}^{i}=\Gamma _{a}^{i}+\beta K_{a}^{i} where K_{a}^{i}=K_{{ab}}e^{{bi}} and K_{{ab}} is the extrinsic curvature. With 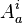A_{a}^{i} as the configuration variable, the conjugate momentum is the densitized triad 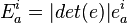E_{a}^{i}=|det(e)|e_{a}^{i}. With 3+1 general relativity rewritten as a special type of SU(2) Yang-Mills gauge theory, it allows the importation of non-perturbative techniques used in Quantum chromodynamics to canonical quantum general relativity.

See also

References

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.